一. 本章目标
- 理解标量场与矢量场的概念
- 掌握矢量场的散度和旋度、标量场的梯度的计算公式和方法
- 掌握和应用散度定理和斯托克斯定理
- 理解亥姆霍兹定理的重要意义
三度&三定理:梯度、散度、旋度&高斯散度定理、斯托克斯定理、亥姆霍兹定理
二. 矢量代数及其代数运算
1.矢量
矢量$\boldsymbol{A}$可以表示为$\boldsymbol{A}=\boldsymbol{e_A}A$
其中$A$表示矢量$\boldsymbol{A}$的大小,$e$表示矢量$\boldsymbol{A}$的方向
一个矢量对应三个标量场
$$ \boldsymbol{A}=\boldsymbol{e_x}A_x+\boldsymbol{e_y}A_y+\boldsymbol{e_z}A_z $$
2.矢量的加减法
$$ \begin{aligned} \boldsymbol{A}+\boldsymbol{B}&=\boldsymbol{e_x}(A_x+B_x)+\boldsymbol{e_y}(A_y+B_y)+\boldsymbol{e_z}(A_z+B_z) \\ \boldsymbol{A}-\boldsymbol{B}&=\boldsymbol{A}+(-\boldsymbol{B}) \end{aligned} $$
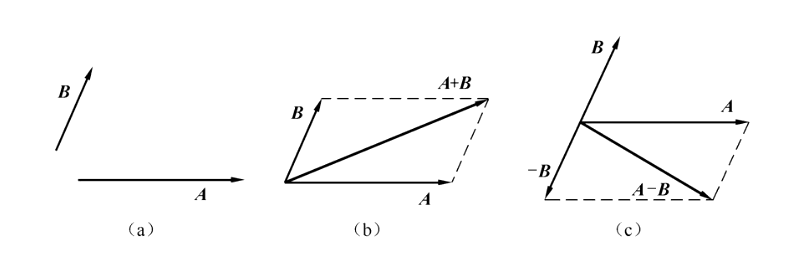
3.标量与矢量相乘
$\boldsymbol{A}$方向不变,大小变为原来的$k$倍.
$$ k\boldsymbol{A}=\boldsymbol{e_x}kA_x+\boldsymbol{e_y}kA_y+\boldsymbol{e_z}kA_z $$
4.矢量的点积
两个矢量的点积是一个标量
$$ \begin{aligned} \boldsymbol{A}\cdot\boldsymbol{B}&=\boldsymbol{A}\boldsymbol{B}\cos{\theta}\\ \boldsymbol{A}\cdot\boldsymbol{B}&=A_xB_x+A_yB_y+A_zB_z \\ \boldsymbol{e_x}\cdot\boldsymbol{e_y}&=0 \boldsymbol{e_x}\cdot\boldsymbol{e_x}=1 \end{aligned} $$
5.矢量的叉积
两个矢量的叉积是一个矢量
大小等于两个矢量的大小与它们夹角$\theta$正弦的乘积
方向垂直于$\boldsymbol{A}$与$\boldsymbol{B}$组成的平面(符合右手螺旋法则)
$$ \boldsymbol{A}\times\boldsymbol{B}=\boldsymbol{e_n}AB\sin{\theta} $$
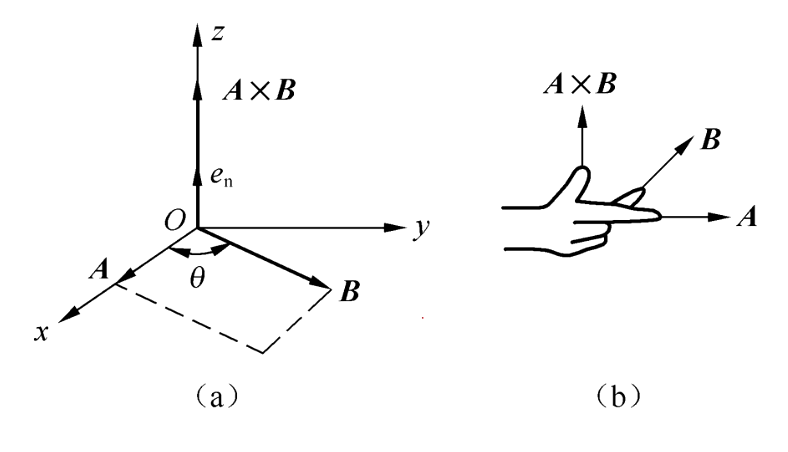
$\boldsymbol{A}\times\boldsymbol{B}$与$\boldsymbol{B}\times\boldsymbol{A}$方向相反
$$ \begin{aligned} &\boldsymbol{A}\times\boldsymbol{B}=\left|\begin{array}{cccc}\boldsymbol{e_x}&\boldsymbol{e_y}&\boldsymbol{e_z}\\ A_x&A_y&A_z \\ B_x&B_y&B_z\end{array}\right|\\ &\boldsymbol{e_x}\times\boldsymbol{e_x}=0\\ &\boldsymbol{e_x}\times\boldsymbol{e_y}=\boldsymbol{e_z}\\ &\boldsymbol{e_y}\times\boldsymbol{e_z}=\boldsymbol{e_x}\\ &\boldsymbol{e_z}\times\boldsymbol{e_x}=\boldsymbol{e_y}\\ &x\rightarrow y\rightarrow z \rightarrow x \rightarrow \cdots \end{aligned} $$
6.矢量叉积的性质
- $\boldsymbol{A}\times\boldsymbol{B}=-\boldsymbol{B}\times\boldsymbol{A}$
- $\boldsymbol{A}\times(\boldsymbol{B}+\boldsymbol{C})=\boldsymbol{A}\times\boldsymbol{B}+\boldsymbol{A}\times\boldsymbol{C}$
- $ \boldsymbol{A}\times(\boldsymbol{B}\times\boldsymbol{C})\neq (\boldsymbol{A}\times\boldsymbol{B})\times\boldsymbol{C}$
标量三重积(Scalar Triple Product)
$\boldsymbol{A}\cdot(\boldsymbol{B}\times\boldsymbol{C})=\boldsymbol{B}\cdot(\boldsymbol{C}\times\boldsymbol{A})=\boldsymbol{C}\cdot(\boldsymbol{A}\times\boldsymbol{B})$
矢量三重积(Vector Triple Product)
$\boldsymbol{A}\times(\boldsymbol{B}\times\boldsymbol{C})=\boldsymbol{B}(\boldsymbol{C}\cdot\boldsymbol{A})-\boldsymbol{C}(\boldsymbol{A}\cdot\boldsymbol{B})$
7.标量、矢量、场
标量(Scalar):只有大小没有方向
矢量(Fector):有大小也有方向
场(Field):在指定的时刻,空间每一点如果可以用一个量唯一地描述,则该量函数定出了场。
(1) 场的重要特性
- 占有一个空间,客观存在
- 可以用数学模型来描述
- 除个别点和表面,物理状态连续
- 分为静态场和动态场
(2) 标量场
如温度场、电位场、高度场。
(3) 矢量场
如速度场、电场、磁场。
三. 矢量场的散度
1.矢量场的矢量线
矢量场的矢量线又称为力线、流线、通量线等。
矢量线图上每一点处的切线应当是该点矢量场的方向。
矢量场$\boldsymbol{A}$可以表示为
$$ \boldsymbol{A}=\boldsymbol{e_x}A_x(x,y,z)+\boldsymbol{e_y}A_y(x,y,z)+\boldsymbol{e_z}A_z(x,y,z) $$
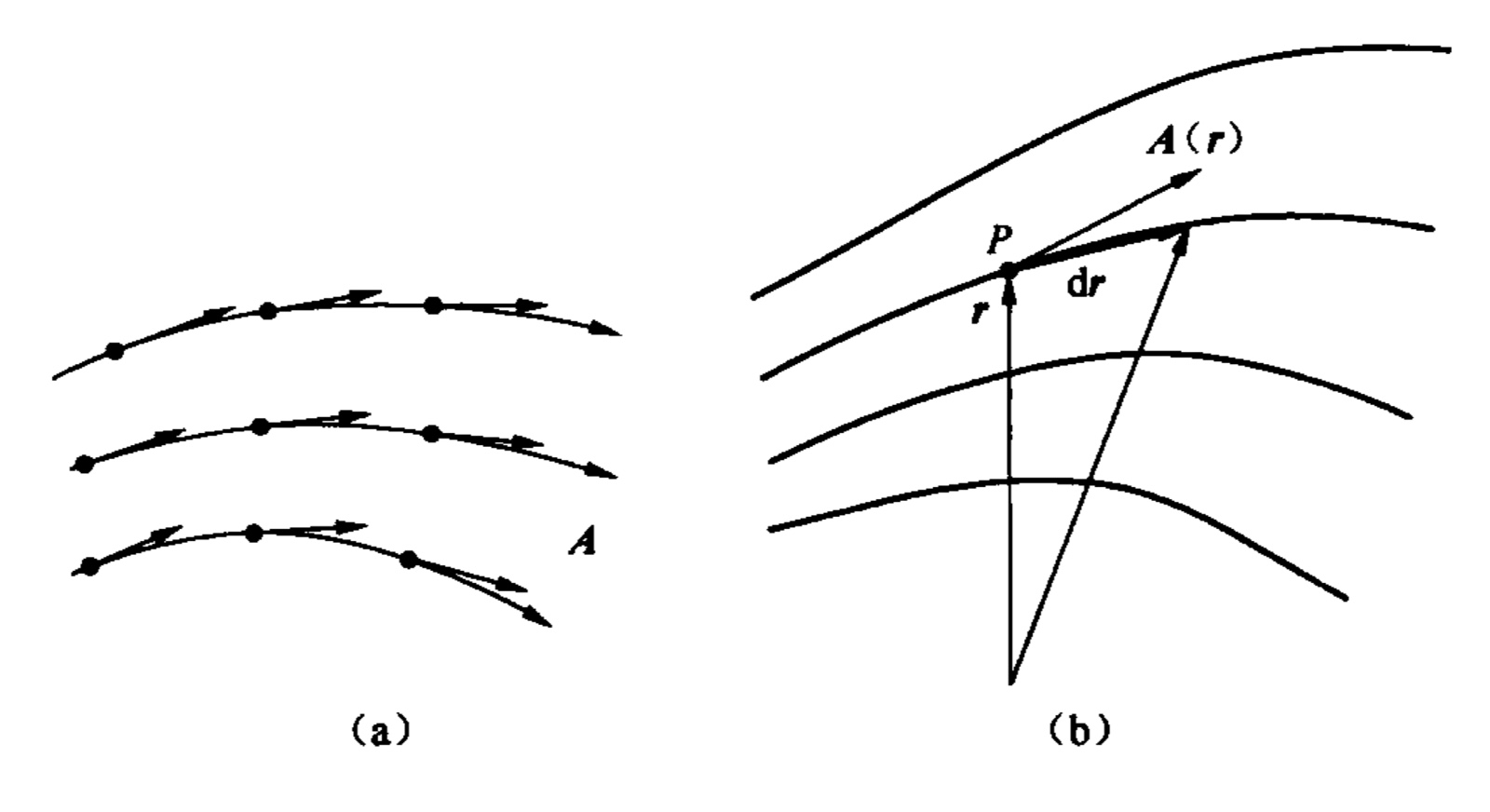
2.矢量线满足的微分方程
$\boldsymbol{A}\times d\boldsymbol{l}=0$
$\boldsymbol{A}\times d\boldsymbol{l}=\left|\begin{array}{cccc} \boldsymbol{e_x} & \boldsymbol{e_y} & \boldsymbol{e_z} \\ A_x & A_y & A_z\\ dx& dy & dz \end{array}\right| $
展开行列式得到在直角坐标系下矢量线满足的微分方程:
二维场:$\frac{dx}{A_x}=\frac{dy}{A_y}$
三维场:$\frac{dx}{A_x}=\frac{dy}{A_y}=\frac{dz}{A_z} $(矢量线方程)
3.矢量场的通量
矢量场的通量即为垂直于矢量场的单位表面矢量线所穿过的数目
(1) 面元矢量
面元矢量$\mathrm{d}\boldsymbol{S}=\boldsymbol{e_n}\mathrm{d}S$
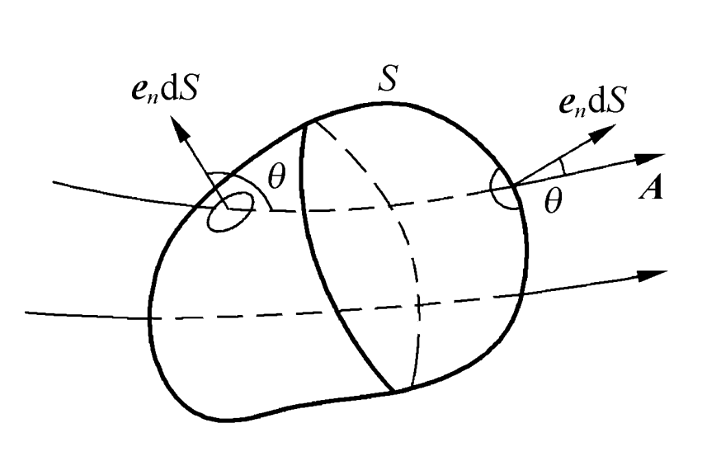
$\boldsymbol{e_n}$的两种取向:
面元$\mathrm{d}\boldsymbol{S}$为开表面上的面元时
设开表面由一条闭合曲线$\mathrm{C}$围成,选择$\mathrm{C}$的环形方向后,用右手螺旋法则确定螺旋前进方向即为$\boldsymbol{e_n}$的方向
面元$\mathrm{d}\boldsymbol{S}$为闭合面上的面元时
$\boldsymbol{e_n}$的方向取闭合面的外法线方向
(2) 通量
矢量$\boldsymbol{A}$沿有向曲面$S$的面积分 $\Phi=\int_S \boldsymbol{A}\mathrm{d}\boldsymbol{S}$ 即为矢量$\boldsymbol{A}$沿有向曲面$S$的通量
若$S$为闭合曲面$\Phi=\oint_S \boldsymbol{A}\mathrm{d}\boldsymbol{S}$
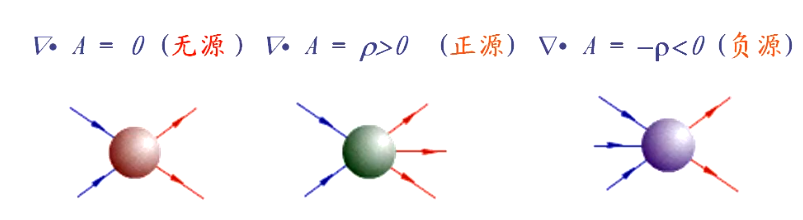
$\Phi>0\Rightarrow$流出的矢量线$>$流入的矢量线$\Rightarrow$闭合曲面内有正源
$\Phi<0\Rightarrow$流出的矢量线$<$流入的矢量线$\Rightarrow$闭合曲面内有负源
$\Phi=0\Rightarrow$闭合曲面内正负源代数和为$0$或没有源
4.矢量场的散度
定义式
$$ \mathrm{div}\boldsymbol{A}=\lim_{\Delta \tau \rightarrow0}\frac{\oint_S \boldsymbol{A}\cdot\mathrm{d}\boldsymbol{S}}{\Delta \tau} $$
计算公式
$$ \mathrm{div}\boldsymbol{A}=\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} $$
哈密顿算子
$$ \begin{aligned} \nabla&=\boldsymbol{e_x}\frac{\partial}{\partial x}+\boldsymbol{e_y}\frac{\partial}{\partial y}+\boldsymbol{e_z}\frac{\partial}{\partial z} \\ \nabla\cdot\boldsymbol{A}&=\mathrm{div}\boldsymbol{A}=\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} \end{aligned} $$
散度的物理意义
- 矢量的散度是一个标量,是空间坐标点的函数
- 散度代表矢量场的通量源的分布特性
5.散度定理
散度定理又称高斯散度定理
矢量场散度的体积分=该矢量穿过包围该体积的封闭曲面的总通量
$$ \oint_{S} \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{S}=\int_{\tau} \nabla \cdot \boldsymbol{A} \mathrm{~d} \tau $$
(e.g.)例题
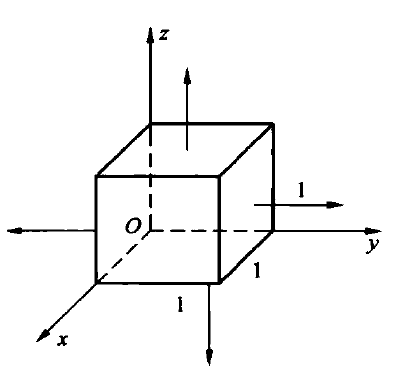
例题 已知$A(x, y, z)=e_{x} x^{2}+e_{y} x y+e_{z} y z$,现有一个边长为1的正方体如图所示,求
- 矢量场$\boldsymbol{A}$的散度
- $\oint_{S} \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{S}$,积分区域为图中的单体立方体
- 验证散度定理
解
$$ \begin{aligned} \nabla \cdot \boldsymbol{A}&=\frac{\partial A_{x}}{\partial x}+\frac{\partial A_{y}}{\partial y}+\frac{\partial A_{z}}{\partial z} \\&=\frac{\partial}{\partial x}\left(x^{2}\right)+\frac{\partial}{\partial y}(x y)+\frac{\partial}{\partial z}(y z)=3 x+y \end{aligned} $$
左面:
$$ y=0, \mathrm{~d} S=-\boldsymbol{e}_{y} \mathrm{~d} x \mathrm{~d} z, A \cdot \mathrm{d} S=\left(\boldsymbol{e}_{y} x y\right) \cdot\left(-\boldsymbol{e}_{y} \mathrm{~d} x \mathrm{~d} z\right)=0 $$
右面:
$$ y=1, \mathrm{~d} S=\boldsymbol{e}_{y} \mathrm{~d} x \mathrm{~d} z, \boldsymbol{A} \cdot \mathrm{d} S=\left(\boldsymbol{e}_{y} x y\right) \cdot\left(\boldsymbol{e}_{y} \mathrm{~d} x \mathrm{~d} z\right)=x \mathrm{~d} x \mathrm{~d} z $$
从左右面穿出的总通量为
$$ \int_{0}^{1} \int_{0}^{1} 0 \mathrm{~d} x \mathrm{~d} z+\int_{0}^{1} \int_{0}^{1} x \mathrm{~d} x \mathrm{~d} z=0+\frac{1}{2}=\frac{1}{2} $$
前面、后面、上面、下面同理
计算得
$$ \oint_{S} A \cdot \mathrm{d} S=\frac{1}{2}+1+\frac{1}{2}=2 $$
$$ \begin{aligned} \int_{\tau} \nabla \cdot \boldsymbol{A} \mathrm{d} \tau&=\int_{0}^{1} \int_{0}^{1} \int_{0}^{1}(3 x+y) \mathrm{d} x \mathrm{~d} y \mathrm{~d} z=2 \\ \int_{\tau} \nabla \cdot A \mathrm{~d} \tau&=\oint_{S} A \cdot \mathrm{d} S=2 \end{aligned} $$
因此高斯散度定理成立
四. 矢量场的旋度
1.矢量场的环流
矢量场$\boldsymbol{A}$绕场中某闭合路径$\mathrm{C}$的线积分为矢量场$\boldsymbol{A}$的环流
$$ \oint_{C} A \cdot \mathrm{d} l=\oint_{C} A \cos \theta \mathrm{d} l $$
2.线元矢量
$$ \begin{aligned} \mathrm{d} \boldsymbol{l}&=\boldsymbol{e_{x}} \mathrm{~d} x+\boldsymbol{e_{y}} \mathrm{~d} y+\boldsymbol{e_{z}} \mathrm{~d} z \\ \\ \oint_{C} A \cdot \mathrm{d} l &=\oint_{C}\left(e_{x} A_{x}+e_{y} A_{y}+e_{z} A_{z}\right) \cdot\left(e_{x} \mathrm{~d} x+e_{y} \mathrm{~d} y+e_{z} \mathrm{~d} z\right) \\ &=\oint_{C}\left(A_{x} \mathrm{~d} x+A_{y} \mathrm{~d} y+A_{z} \mathrm{~d} z\right) \end{aligned} $$
3.矢量场的环流面密度
$$ \lim _{\Delta S \rightarrow 0} \frac{\oint_{C} A \cdot \mathrm{d} l}{\Delta S} $$
4.矢量场的旋度
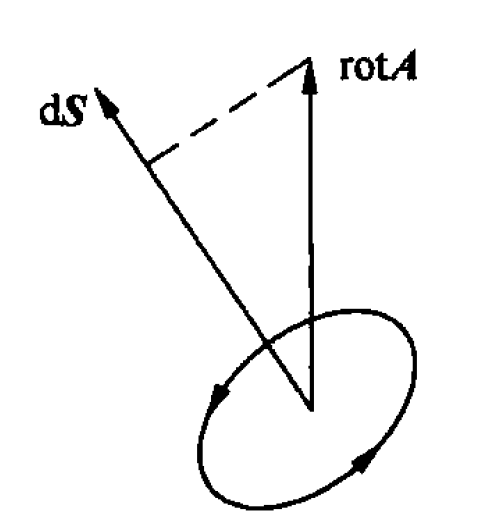
(1) 旋度的定义
因为面积元$\Delta S$与漩涡面可能存在夹角
环流面密度极限值的大小与面积元$\Delta S$的方向有关
当面积元$\Delta S$与漩涡面处于同一平面时
环流面密度最大,即为矢量场的旋度
$$ \operatorname{rot} A=\lim _{\Delta S \rightarrow 0} \frac{\oint_{C} A \cdot \mathrm{d} l}{\Delta S} $$
(2) 旋度的计算式
$$ \begin{aligned} \operatorname{rot} A&=e_{x}\left(\frac{\partial A_{z}}{\partial y}-\frac{\partial A_{y}}{\partial z}\right)+e_{y}\left(\frac{\partial A_{x}}{\partial z}-\frac{\partial A_{z}}{\partial x}\right)+e_{z}\left(\frac{\partial A_{y}}{\partial x}-\frac{\partial A_{x}}{\partial y}\right) \\ \\ \operatorname{rot} A&=\nabla \times A=\left|\begin{array}{lll} \boldsymbol{e}_{x} & \boldsymbol{e}_{y} & \boldsymbol{e}_{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ A_{x} & A_{y} & A_{z} \end{array}\right| \end{aligned} $$
(3) 旋度的性质
旋度的散度恒为0
$$ \begin{aligned} \nabla \cdot \nabla \times \boldsymbol{A} &=\nabla \cdot\left[\boldsymbol{e}_{x}\left(\frac{\partial A_{z}}{\partial y}-\frac{\partial A_{y}}{\partial z}\right)+\boldsymbol{e}_{y}\left(\frac{\partial A_{x}}{\partial z}-\frac{\partial A_{z}}{\partial x}\right)+e_{z}\left(\frac{\partial A_{y}}{\partial x}-\frac{\partial A_{x}}{\partial y}\right)\right] \\ &=\frac{\partial}{\partial x}\left(\frac{\partial A_{z}}{\partial y}-\frac{\partial A_{y}}{\partial z}\right)+\frac{\partial}{\partial y}\left(\frac{\partial A_{x}}{\partial z}-\frac{\partial A_{z}}{\partial x}\right)+\frac{\partial}{\partial z}\left(\frac{\partial A_{y}}{\partial x}-\frac{\partial A_{x}}{\partial y}\right) \\ &=0 \end{aligned} $$
关于此性质的应用:
对于无散场$\boldsymbol{B}$,有$\nabla \cdot \boldsymbol{B}=0$
总可以把它表示为另一矢量场的旋度
即$\boldsymbol{B}=\nabla \times \boldsymbol{A}$
5.斯托克斯定理
$$ \int_{S} \nabla \times \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{S}=\oint_{C} \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{l} $$
(e.g.) 例题
矢量场$\boldsymbol{A}(x, y)=\boldsymbol{e_{x}} x^{2}+\boldsymbol{e_{y}} x y^{2}$,抛物线$y^{2}=x$,闭合曲线$C$路径如图,求
(1)矢量场$\boldsymbol{A}$的旋度
(2)环流$\oint_{C} A \cdot \mathrm{d} l$
(3)验证斯托克斯定理

解:
(1)
$$ \nabla \times A=\left|\begin{array}{ccc} e_{x} & e_{y} & e_{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ x^{2} & x y^{2} & 0 \end{array}\right|=e_{z} y^{2} $$
(2)
$$ \begin{aligned} \vec{A} \cdot d \vec{l} &=\left(\overrightarrow{e_{x}} x^{2}+\overrightarrow{e_{y}} x y^{2}\right) \cdot\left(\overrightarrow{e_{x}} d x+\overrightarrow{e_{y}} d y\right) \\ &=x^{2} d x+x y^{2} d y \\ \\ \oint_{c} \vec{A} d \vec{l}&=\oint_{c}\left(x^{2} d x+x y^{2} d y\right) \\ &=\int_{0}^{2} x^{2} d x+\int_{0}^{\sqrt{2}} 2 y^{2} d y+\int_{2}^{0}\left(x^{2} d x+x^{2} \cdot x d \sqrt{x}\right) \\ &=\frac{8}{15} \sqrt{2} \end{aligned} $$
(3)
$$ \begin{aligned} &\nabla \times \vec{A}=\overrightarrow{e_{z}} y^{2} ,\quad d \vec{S}=\overrightarrow{e_{n}} d S=\overrightarrow{e_{z}} d x d y . \\ &\nabla \times \vec{A} \cdot d \vec{S}=\overrightarrow{e_{z}} y^{2} \cdot \overrightarrow{e_{z}} d x d y=y^{2} d x d y . \\ &\int_{S} \nabla \times \vec{A} \cdot d \vec{S}=\iint y^{2} d x d y =\int_{0}^{\sqrt{2}}\left(\int_{y^{2}}^{2} d x\right) y^{2} d y=\frac{8}{15} \sqrt{2} \end{aligned} $$
五. 标量场的梯度
标量场是仅用大小就能够完全表征的场,如标量场$u(x, y, z)$
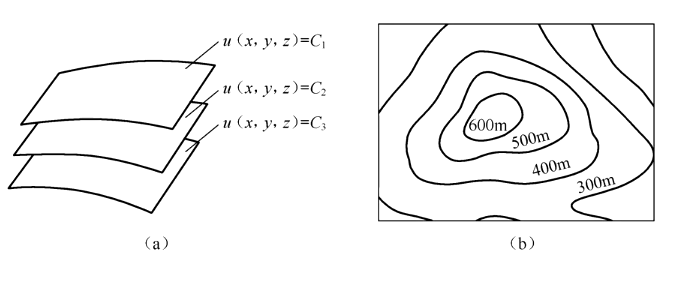
1.标量场的等值面
标量函数$u(x, y, z)$中相等的点构成的曲面称为等值面
$$ u(x, y, z)=c $$
2.标量场的梯度
梯度是表示标量最大空间增长率的大小和方向的矢量
设标量场$u(x,y,z)$,从场中某点移动至另一点,场从$u$变化到$u+\mathrm{d}u$,增量$\mathrm{d}u$
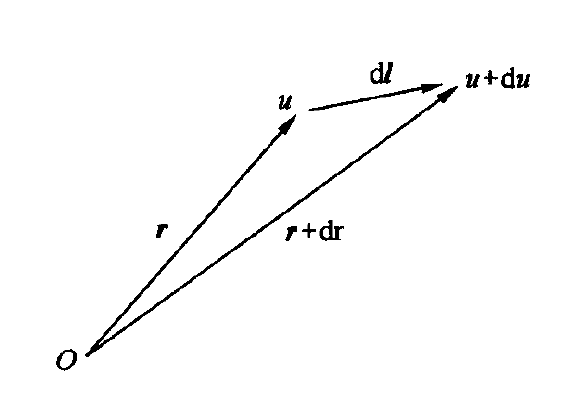
$$ \begin{aligned} \mathrm{d} u&=\frac{\partial u}{\partial x} \mathrm{~d} x+\frac{\partial u}{\partial y} \mathrm{~d} y+\frac{\partial u}{\partial z} \mathrm{~d} z \\ &=(e_{x} \frac{\partial u}{\partial x}+e_{y} \frac{\partial u}{\partial y}+e_{z} \frac{\partial u}{\partial z} )\cdot( e_{x} \mathrm{~d} x+e_{y} \mathrm{~d} y+e_{z} \mathrm{~d} z) \\ &=\nabla u \cdot \mathrm{d} \boldsymbol{l} \\ \\ \nabla u&= \boldsymbol{e_{x}} \frac{\partial u}{\partial x}+\boldsymbol{e_{y}} \frac{\partial u}{\partial y}+\boldsymbol{e_{z}} \frac{\partial u}{\partial z} \end{aligned} $$
$\nabla u$即为标量场$u$的梯度,也作$\mathrm{grad}\ u$
梯度是与等值面垂直的一个矢量
(等值面的法向为$u$的最大变化率方向)
大小是沿等值面法向的$u$的变化率
3.方向导数
$\frac{\partial u}{\partial l}$为$u$沿$\mathrm{d}l$方向的变化率,称为标量场$u$沿方向$l$的方向导数
$u$沿某个方向的方向导数等于$u$的梯度在这个方向的投影
$$ \frac{\partial u}{\partial l}=|\nabla u|_{l}=\nabla u \cdot \boldsymbol{e_{l}} $$
(e.g.) 例题
标量场$u(x, y, z)=\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2}$,求点$A(1,0,1)$的梯度和沿方向$\boldsymbol{l}=e_{x} 2+e_{y} 1+e_{z} 2$的方向导数。
解:
$$ \begin{aligned} \left.\nabla u\right|_{(1,0,1)} &=e_{x} \frac{\partial u}{\partial x}+e_{y} \frac{\partial u}{\partial y}+\left.e_{z} \frac{\partial u}{\partial z}\right|_{(1,0,1)} \\ &=e_{x} \frac{x}{\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2}}+e_{y} \frac{y}{\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2}}+\left.e_{z} \frac{z}{\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2}}\right|_{(1,0,1)} \\ &=e_{x} \frac{1}{\sqrt{2}}+e_{z} \frac{1}{\sqrt{2}} \end{aligned} $$
$\boldsymbol{l}$方向的单位矢量$\boldsymbol{e_l}$为:
$$ \boldsymbol{e_{l}}=\frac{\boldsymbol{l}}{|\boldsymbol{l}|}=\frac{e_{x} 2+e_{y} 1+e_{x} 2}{\sqrt{2^{2}+1^{2}+2^{2}}}=\frac{1}{3}\left(e_{x} 2+e_{y} 1+e_{z} 2\right) $$
所以所求方向导数为:
$$ \begin{aligned} \left.\frac{\partial u}{\partial l}\right|_{(1,0,1)}&=\left.\nabla u \cdot e_{l}\right|_{(1,0,1)} \\ &=\left(e_{z} \frac{1}{\sqrt{2}}+e_{z} \frac{1}{\sqrt{2}}\right) \cdot \frac{1}{3}\left(e_{x} 2+e_{y} 1+e_{x} 2\right) \\ &=\frac{2 \sqrt{2}}{3} \end{aligned} $$
4.梯度的性质
梯度的旋度恒为0
证明:
$$ \begin{aligned} \nabla \times \nabla u &=\left(e_{x} \frac{\partial}{\partial x}+e_{y} \frac{\partial}{\partial y}+e_{z} \frac{\partial}{\partial z}\right) \times\left(e_{x} \frac{\partial u}{\partial x}+e_{y} \frac{\partial u}{\partial y}+e_{z} \frac{\partial u}{\partial z}\right) \\ &=e_{x}\left(\frac{\partial}{\partial y} \frac{\partial u}{\partial z}-\frac{\partial}{\partial z} \frac{\partial u}{\partial y}\right)+e_{y}\left(\frac{\partial}{\partial z} \frac{\partial u}{\partial x}-\frac{\partial}{\partial x} \frac{\partial u}{\partial z}\right)+e_{z}\left(\frac{\partial}{\partial x} \frac{\partial u}{\partial y}-\frac{\partial}{\partial y} \frac{\partial u}{\partial x}\right) \\ &=0 \end{aligned} $$
对于无旋场$\boldsymbol{B}$,总可以把它表示为一个标量场的梯度
$$ \nabla \times \boldsymbol{B}=0 \Longrightarrow \boldsymbol{B}=\nabla \boldsymbol{u} $$
5.拉普拉斯算子
$$ \begin{aligned} \nabla^{2} u&=\nabla \cdot \nabla u \\ \nabla^{2} u&=\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}+\frac{\partial^{2} u}{\partial z^{2}} \end{aligned} $$
六. 亥姆霍兹定理
亥姆霍兹定理 在空间有限区域内有一矢量场$\boldsymbol{F}$,若已知它的散度、旋度和边界条件,则该矢量场就唯一确定了。即一个矢量场所具有的的特性完全由它的散度和旋度确定。
如果一个矢量场$\boldsymbol{F}$既有散度也有旋度,则可以写为
$$ \boldsymbol{F}=\boldsymbol{F_{1}}+\boldsymbol{F_{2}} $$
其中$\boldsymbol{F_1}$是一个只有散度的无旋场
其中$\boldsymbol{F_2}$是一个只有旋度的无散场
七. 坐标系
1.直角坐标系
| 项目 | 表达方式 |
|---|---|
| 线元矢量 | $\mathrm{d} l=e_{x} \mathrm{~d} x+e_{y} \mathrm{~d} y+e_{z} \mathrm{~d} z$ |
| 面元矢量 | $\mathrm{d} S=e_{x} \mathrm{~d} S_{z}+e_{y} \mathrm{~d} S_{y}+e_{z} \mathrm{~d} S_{z}$$=e_{x} \mathrm{~d} y \mathrm{~d} z+e_{y} \mathrm{~d} z \mathrm{~d} x+e_{z} \mathrm{~d} x \mathrm{~d} y$ |
| 体积元标量 | $\mathrm{d} \tau=\mathrm{d} x \mathrm{~d} y \mathrm{~d} z$ |
| 哈密顿算子 | $\nabla=e_{x} \frac{\partial}{\partial x}+e_{y} \frac{\partial}{\partial y}+e_{z} \frac{\partial}{\partial z}$ |
2.圆柱坐标系

圆柱坐标系中的点用3个自变量$(r, \varphi, z)$表示
圆柱坐标系中的矢量可以用3个分量表示
$$ A=e_{r} A_{r}+e_{\varphi} A_{\varphi}+e_{z} A_{z} $$
圆柱坐标系与直角坐标系自变量之间的关系
$$ \left.\begin{array}{l} x=r \cos \varphi, y=r \sin \varphi, z=z \\ r=\sqrt{x^{2}+y^{2}}, \tan \varphi=y / x \end{array}\right\} $$
圆柱坐标系中的3个单位矢量为$e_{r}$、$e_{\varphi}$和$e_{z}$
| $e_{z}$ | 常矢量 |
|---|---|
| $e_{r}$ | 变矢量 是自变量$\varphi$的函数 |
| $e_{\varphi}$ | 变矢量 是自变量$\varphi$的函数 |
$$ \left.\begin{array}{l} e_{r} \cdot e_{r}=e_{\varphi} \cdot e_{\varphi}=e_{z} \cdot e_{z}=1 \\ e_{r} \cdot e_{\varphi}=e_{\varphi} \cdot e_{z}=e_{z} \cdot e_{r}=0 \\ e_{z}=e_{r} \times e_{\varphi}, e_{r}=e_{\varphi} \times e_{z}, e_{\varphi}=e_{z} \times e_{r} \end{array}\right\} $$
它们与直角坐标系单位矢量的关系为
$$ \begin{aligned} &\boldsymbol{e}_{r}=\boldsymbol{e}_{x} \cos \varphi+\boldsymbol{e}_{y} \sin \varphi \\ &\boldsymbol{e}_{\varphi}=-\boldsymbol{e}_{x} \sin \varphi+\boldsymbol{e}_{y} \cos \varphi \end{aligned} $$
$e_{r} 、 e_{\varphi}$ 对自变量 $\varphi$ 的微分为
$$ \left.\begin{array}{l} \frac{d e_{r}}{d \varphi}=-e_{x} \sin \varphi+e_{y} \cos \varphi=e_{\varphi} \\ \frac{d e_{\varphi}}{d \varphi}=-e_{x} \cos \varphi-e_{y} \sin \varphi=-e_{r} \end{array}\right\} $$
空间一点的位置可以用位置矢量$\boldsymbol{r}$表示。在圆柱坐标系中
$$ r=e_{r} r+e_{z} z \\ \mathrm{d} r=e_{r} \mathrm{~d} r+e_{\varphi} r \mathrm{~d} \varphi+e_{z} \mathrm{~d} z $$
线元矢量、面元矢量和体积元:
$$ \begin{aligned} \mathrm{d} l &=e_{r} h_{r} \mathrm{~d} r+e_{\varphi} h_{\varphi} \mathrm{d} \varphi+e_{z} h_{z} \mathrm{~d} z \\ &=e_{r} \mathrm{~d} r+e_{\varphi} r \mathrm{~d} \varphi+e_{z} \mathrm{~d} z \\ \\ \mathrm{~d} S &=e_{r} h_{\varphi} h_{z} \mathrm{~d} \varphi \mathrm{d} z+e_{\varphi} h_{z} h_{r} \mathrm{~d} z \mathrm{~d} r+e_{z} h_{r} h_{\varphi} \mathrm{d} r \mathrm{~d} \varphi \\ &=e_{r} r \mathrm{~d} \varphi \mathrm{d} z+e_{\varphi} \mathrm{d} z \mathrm{~d} r+e_{z} r \mathrm{~d} r \mathrm{~d} \varphi \\ \\ \mathrm{d} \tau &=h_{r} h_{\varphi} h_{z} \mathrm{~d} r \mathrm{~d} \varphi \mathrm{d} z=r \mathrm{~d} r \mathrm{~d} \varphi \mathrm{d} z \end{aligned} $$
哈密顿算子:
$$ \begin{aligned} \nabla &=e_{r} \frac{\partial}{h_{r} \partial r}+e_{\varphi} \frac{\partial}{h_{\varphi} \partial \varphi}+e_{z} \frac{\partial}{h_{z} \partial z} \\ &=e_{r} \frac{\partial}{\partial r}+e_{\varphi} \frac{\partial}{r}+e_{z} \frac{\partial}{\partial z} \end{aligned} $$
梯度:
$$ \nabla u=e_{r} \frac{\partial u}{\partial r}+e_{\varphi} \frac{\partial u}{r \partial \varphi}+e_{z} \frac{\partial u}{\partial z} $$
$A=e_{r} A_{r}+e_{\varphi} A_{\varphi}+e_{z} A_{z}$的散度:
$$ \begin{aligned} \nabla \cdot A=&\left(e_{r} \frac{\partial}{\partial r}+e_{\varphi} \frac{\partial}{r \partial \varphi}+e_{z} \frac{\partial}{\partial z}\right) \cdot\left(e_{r} A_{r}+e_{\varphi} A_{\varphi}+e_{z} A_{z}\right) \\ =& e_{r} \cdot\left(e_{r} \frac{\partial A_{r}}{\partial r}+e_{\varphi} \frac{\partial A_{\varphi}}{\partial r}+e_{z} \frac{\partial A_{z}}{\partial r}\right)+ e_{\varphi} \cdot \frac{1}{r}\left(e_{r} \frac{\partial A_{r}}{\partial \varphi}+A_{r} \frac{\partial e_{r}}{\partial \varphi}+e_{\varphi} \frac{\partial A_{\varphi}}{\partial \varphi}+A_{\varphi} \frac{\partial e_{\varphi}}{\partial \varphi}+e_{z} \frac{\partial A_{z}}{\partial \varphi}\right)+ e_{z} \cdot\left(e_{r} \frac{\partial A_{r}}{\partial z}+e_{\varphi} \frac{\partial A_{\varphi}}{\partial z}+e_{z} \frac{\partial A_{z}}{\partial z}\right) \\ =&\frac{1}{r} \frac{\partial}{\partial r}\left(r A_{r}\right)+\frac{1}{r} \frac{\partial A_{\varphi}}{\partial \varphi}+\frac{\partial A_{z}}{\partial z} \end{aligned} $$
$A=e_{r} A_{r}+e_{\varphi} A_{\varphi}+e_{z} A_{z}$的旋度:
$$ \begin{aligned} \nabla \times \boldsymbol{A}&=e_{r}\left(\frac{1}{r} \frac{\partial A_{z}}{\partial \varphi}-\frac{\partial A_{\varphi}}{\partial z}\right)+e_{\varphi}\left(\frac{\partial A_{r}}{\partial z}-\frac{\partial A_{z}}{\partial r}\right)+e_{z} \frac{1}{r}\left[\frac{\partial}{\partial r}\left(r A_{\varphi}\right)-\frac{\partial A_{r}}{\partial \varphi}\right] \\ \\ \nabla \times \boldsymbol{A}&=\left|\begin{array}{lll} \frac{\boldsymbol{e}_{r}}{r} & e_{\varphi} & \frac{e_{z}}{r} \\ \frac{\partial}{\partial r} & \frac{\partial}{\partial \varphi} & \frac{\partial}{\partial z} \\ A_{r} & r A_{\varphi} & A_{z} \end{array}\right| \end{aligned} $$
3.球坐标系
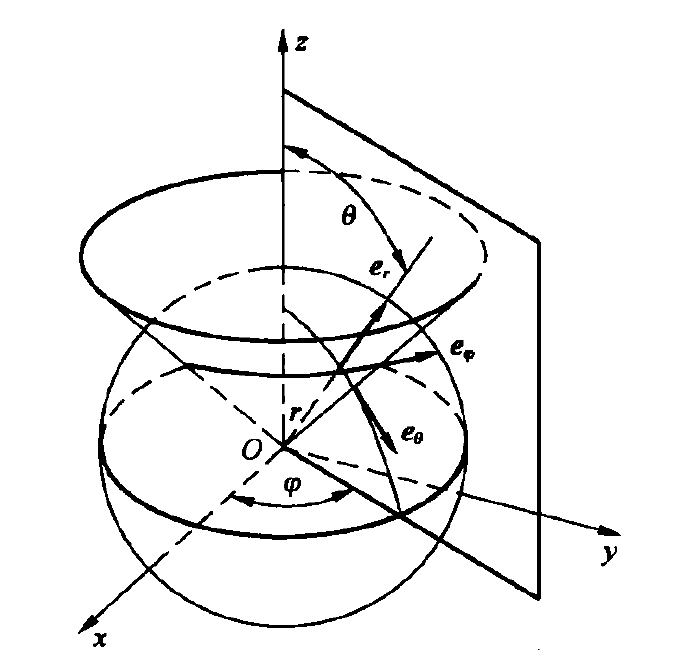
球坐标系中的点用3个自变量表示$(r, \theta, \varphi)$
球坐标系与直角坐标系自变量之间的关系为:
$$ \left.\begin{array}{l} x=r \sin \theta \cos \varphi, y=r \sin \theta \sin \varphi, z=r \cos \theta \\ r=\sqrt{x^{2}+y^{2}+z^{2}}, \tan \varphi=y / x \end{array}\right\} $$
球坐标系中的矢量用3个分量表示
$$ A=e_{r} A_{r}+e_{\theta} A_{\theta}+e_{\varphi} A_{\varphi} $$
$e_{r} 、 e_{\theta}$和$e_{\varphi}$是自变量 $\theta$和$\varphi$的函数, 为变矢量
$$ \left.\begin{array}{l} e_{r} \cdot e_{r}=e_{\theta} \cdot e_{\theta}=e_{\varphi} \cdot e_{\varphi}=1 \\ e_{r} \cdot e_{\theta}=e_{\theta} \cdot e_{\varphi}=e_{\varphi} \cdot e_{r}=0 \\ e_{r}=e_{\theta} \times e_{\varphi}, e_{\theta}=e_{\varphi} \times e_{r}, e_{\varphi}=e_{r} \times e_{\theta} \end{array}\right\} $$
$$ \left.\begin{array}{l} e_{r}=e_{x} \sin \theta \cos \varphi+e_{y} \sin \theta \sin \varphi+e_{z} \cos \theta \\ e_{\theta}=e_{x} \cos \theta \cos \varphi+e_{y} \cos \theta \sin \varphi-e_{z} \sin \theta \\ e_{\varphi}=-e_{z} \sin \varphi+e_{y} \cos \varphi \end{array}\right\} $$
$$ \left.\begin{array}{l} \frac{\partial e_{r}}{\partial \theta}=e_{\theta}, \frac{\partial e_{r}}{\partial \varphi}=e_{\varphi} \sin \theta \\ \frac{\partial e_{\theta}}{\partial \theta}=-e_{r}, \frac{\partial e_{\theta}}{\partial \varphi}=e_{\varphi} \cos \theta \\ \frac{\partial e_{\varphi}}{\partial \theta}=0, \frac{\partial e_{\varphi}}{\partial \varphi}=-e_{r} \sin \theta-e_{\theta} \cos \theta \end{array}\right\} $$
线元矢量、面元矢量和体积元为:
$$ \begin{aligned} &\mathrm{d} l=e_{r} \mathrm{~d} r+e_{\theta} r \mathrm{~d} \theta+e_{\varphi} r \sin \theta \mathrm{d} \varphi \\ &\mathrm{d} S=e_{r} r^{2} \sin \theta \mathrm{d} \theta \mathrm{d} \varphi+e_{\theta} r \sin \theta \mathrm{d} \varphi \mathrm{d} r+e_{\varphi} r \mathrm{~d} r \mathrm{~d} \theta \\ &\mathrm{d} \tau=r^{2} \sin \theta \mathrm{d} r \mathrm{~d} \theta \mathrm{d} \varphi \end{aligned} $$
哈密顿算子:
$$ \nabla=e_{r} \frac{\partial}{\partial r}+e_{\theta} \frac{1}{r} \frac{\partial}{\partial \theta}+e_{\varphi} \frac{1}{r \sin \theta} \frac{\partial}{\partial \varphi} $$
梯度:
$$ \nabla \cdot A=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} A_{r}\right)+\frac{1}{r \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta A_{\theta}\right)+\frac{1}{r \sin \theta} \frac{\partial A_{\varphi}}{\partial \varphi} $$
旋度:
$$ \nabla \times A=\left|\begin{array}{ccc} \frac{e_{r}}{r^{2} \sin \theta} & \frac{e_{\theta}}{r \sin \theta} & \frac{e_{\varphi}}{r} \\ \frac{\partial}{\partial r} & \frac{\partial}{\partial \theta} & \frac{\partial}{\partial \varphi} \\ A_{r} & r A_{\theta} & r \sin \theta A_{\varphi} \end{array}\right| $$
1 条评论
学完后半年回来评论,总结的很棒哇