实验目的

加深对脉冲响应不变法设计IIR 数字滤波器基本方法的了解。
掌握使用模拟滤波器原型进行脉冲响应变换的方法。
了解MATLAB 有关脉冲响应变换的子函数。

实验环境

Windows 11, MATLAB2021a

示例程序

用脉冲响应不变法设计巴特沃斯数字带通滤波器

采用脉冲响应不变法设计一个巴特沃斯数字带通滤波器，要求带通$ω_{p1}=0.3π$$,ω_{p2}=0.7π$,$R_P=1dB$;$ω_{s1}=0.1π$,$ω_{s2}=0.9π$,$A_s=15dB$，滤波器采样频率$F_s=2000Hz$。试求解：
(1)显示数字滤波器的幅频响应、相位响应和零极点分布图。
(2)求出巴特沃斯数字带通滤波器传输函数的直接型表达式。
(3)比较它和实验内容里的第2个例子切比雪夫带通滤波器的异同点（从数字滤波器的阶次、数字滤波器的特点性能、零极点图分布等方面入手）。

%% 数字滤波器各项指标配置
wp1=0.3*pi;wp2=0.7*pi; %数字滤波器的通带截止频率
ws1=0.1*pi;ws2=0.9*pi; %数字滤波器的阻带截止频率
Rp=1;As=15;%输入滤波器的通阻带衰减指标
ripple=10^(-Rp/20); %计算通带衰减对应的幅度值
Attn=10^(-As/20); %计算阻带衰减对应的幅度值

%% 转换为模拟滤波器指标
Fs=2000;T=1/Fs;
Omagp1=wp1*Fs;Omagp2=wp2*Fs;%模拟滤波器的通带截止频率
Omagp=[Omagp1,Omagp2];
Omags1=ws1*Fs;Omags2=ws2*Fs;%模拟滤波器的阻带截止频率
Omags=[Omags1,Omags2];
bw=Omagp2-Omagp1;%模拟通带带宽
w0=sqrt(Omagp1*Omagp2);%中心频率

%% 模拟原型滤波器计算
[n,Omagc]=buttord(Omagp,Omags,Rp,As,'s'); %计算阶数n和截止频率
[z0,p0,k0]=buttap(n); %设计归一化的巴特沃思模拟滤波器
ba1=k0*real(poly(z0)); %求原型滤波器系数b
aa1=real(poly(p0)); %求原型滤波器系数a
[ba,aa]=lp2bp(ba1,aa1,w0,bw); %转换为模拟低通滤波器

%% 用脉冲响应不变法计算数字滤波器系数
[bd,ad]=impinvar(ba,aa,Fs);

%% 求数字系统的频率特性
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H))); %化为分贝值

%% 绘图
subplot(2,2,1),plot(w/pi,abs(H));grid
subplot(2,2,2),plot(w/pi,angle(H)/pi);grid
subplot(2,2,3),plot(w/pi,dbH);grid
subplot(2,2,4),zplane(bd,ad);grid
title('零极点分布图')
axis([-2.5,1.5,-1.1,1.1])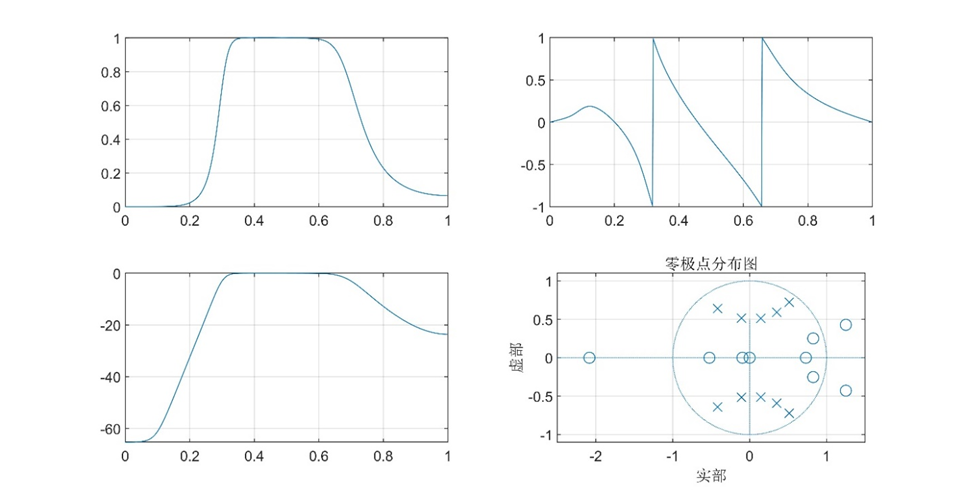

输出图像

bd =
  -0.0000  0.0353  -0.0773  -0.0773  0.3564  -0.3096  0.0050  0.0997  -0.0277  -0.0034

ad =
  1.0000  -0.9832  1.7001  -0.9658  1.3596  -0.6478  0.6715  -0.2121  0.1674  -0.0280  0.0171

根据上述实验结果，得出表达式如下：

$$ H(z)=\frac{0.353 z^{-1}-0.0773 z^{-2}-0.0773 z^{-3}+0.35564 z^{-4}-0.3096 z^{-5}+0.005 z^{-6}+0.0997 z^{-7}-0.0277 z^{-8}-0.0034 z^{-9}}{1-0.9832 z^{-1}+1.7001 z^{-2}-0.9658 z^{-3}+1.5596 z^{-4}-0.6478 z^{-5}+0.6715 z^{-6}-0.2121 z^{-7}+0.1674 z^{-8}-0.0280 z^{-9}+0.0171 z^{-10}} $$