实验目的
- 加深对离散周期序列傅里叶级数(DFS)、离散傅里叶变换(DFT)和快速傅立叶变换(FFT)基本概念的理解。
- 了解有限长序列傅里叶变换(DFT)与周期序列傅里叶级数(DFS)、离散时间傅里叶变换(DTFT)的联系。
- 加深对离散傅里叶变换快速傅立叶变换性质的理解和他们的应用。
- 掌握用MATLAB语言进行变换和逆变换时,所用到的子函数和程序编写的方法。
实验环境
Windows 11, MATLAB2021a
示例程序
绘制序列的(I)DFT和(I)DFS
已知一个信号的序列的主值为x(n)=[0 1 2 3 2 1 0],将x(n)周期重复次数为2个周期,求解信号序列:
(1)画出原主值和信号周期序列信号;
(2)画出序列傅里叶变换对应的$|X(k)|$和$\arg[X(k)]$图形;
(3)画出序列傅里叶级数对应的$|\widetilde{X}({k})|$和$\arg [\widetilde{{X}}({k})]$图形;
(4)画出傅里叶逆变换IDFT$[X(k)]$和IDFS图形进行比较。
%%原主值序列及其DFT
xn=[0,1,2,3,2,1,0];%定义序列主值行向量
N=length(xn);%求序列长度
n=0:N-1;%时域离散时间点
k=0:N-1;%频域离散频点
Xk=xn*exp(-1j*2*pi/N).^(n'*k);%DFT运算
x=(Xk*exp(1j*2*pi/N).^(n'*k))/N;%IDFT运算
%% 绘图
subplot(4,2,1);stem(n,xn);
title('原主值 x(n)');
subplot(4,2,7);stem(n,abs(x));
title('IDFT[X(k)]');
subplot(4,2,3);stem(k,abs(Xk));
title('[X(k)]');
subplot(4,2,5);stem(k,angle(Xk));
title('angle[X(k)]');
%% 周期延拓及其DFS
n1=0:2*N-1;%重复次数为两个周期后的时域离散时间点
k1=0:2*N-1;%重复次数为两个周期后的频域离散时间点
xn1=xn(mod(n1,N)+1);%将xn重复两个周期
Xk1=xn*exp(-1j*2*pi/N).^(n'*k1);%DFS运算
y=real((Xk1(1,1:N)*exp(1j*2*pi/N).^(k'*n1))/N);%IDFS运算
%% 绘图
subplot(4,2,2);stem(n1,xn1);
title('周期序列信号');
subplot(4,2,8);stem(n1,y);
title('IDFT[X(k)1]');
subplot(4,2,4);stem(k1,abs(Xk1));
title('[X(k)1]');
subplot(4,2,6);stem(k1,angle(Xk1));
title('angle[X(k)1]');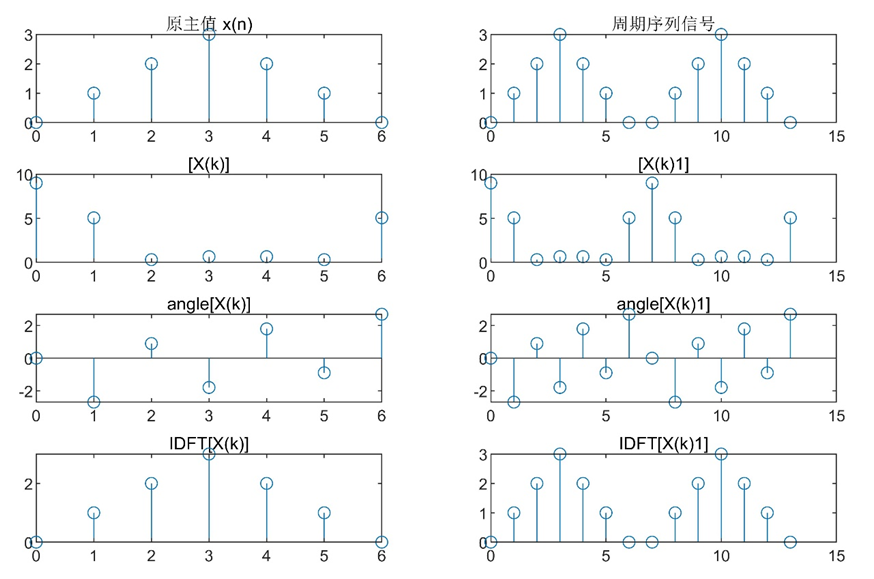
IDFT$[X(k)]$和IDFS图形的比较:
根据实验输出的图像不难发现,对于同一原序列,其IDFS图形为其IDFT图形以自身序列长度为周期进行周期延拓的结果。
圆周卷积
已知有限长序列 $x_1(n)=[\ 5\ 4\ -3\ -2\ ]$,$x_2(n)=[\ 1\ 2\ 3\ 0\ ]$,用DFT求两个序列的圆周卷积$y(n)$,写出其圆周卷积序列的实现过程的程序。
%% 运算
xn1=[1,2,3,0];%定义序列1主值行向量
xn2=[5,4,-3,-2];%定义序列2主值行向量
N=length(xn1);%求序列1的长度
n=0:N-1;%时域离散时间点
k=0:N-1;%频域离散频点
Xk1=xn1*(exp(-1j*2*pi/N)).^(n'*k);%求序列1的DFT
Xk2=xn2*(exp(-1j*2*pi/N)).^(n'*k);%求序列2的DFT
Yk1=Xk1.*Xk2;%两序列频域相乘
yn=Yk1*(exp(1j*2*pi/N)).^(n'*k)/N;%作频域相乘后的IDFT
yn=abs(yn);%求模值
yn2=conv(xn1,xn2);%求两序列的线性卷积
%% 绘图
subplot(2,3,1);stem(n,xn1,'k');
title('xn1')
subplot(2,3,2);stem(n,xn2,'k');
title('xn2')
subplot(2,3,3);stem(yn2,'k');
title('yn2')
subplot(2,3,4);stem(k,abs(Xk1));
title('Xk1')
subplot(2,3,5);stem(k,abs(Xk2));
title('Xk2')
subplot(2,3,6);stem(k,yn);
title('yn');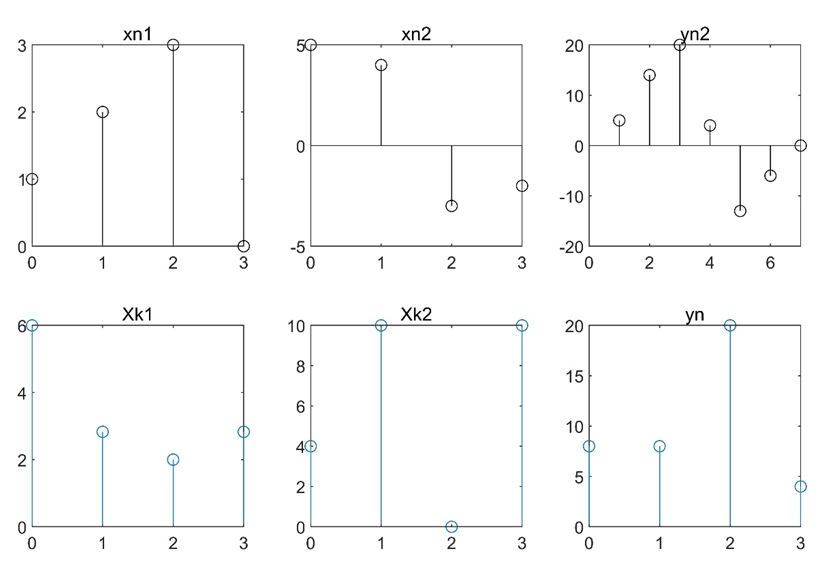
信号相关
Fs=100;N=200;
n=0:N-1;%时域离散时间点
x=2*cos((10*pi*n+2)/Fs);%序列x(n)
x1=x+rands(1,N);%序列x(n)加上噪声
h=cos(10*pi*n/Fs);%序列h(n)
tic %计时开始
y=xcorr(x1,h);%对序列x1(n)和h(n)在时域直接求相关值
t=toc;%计时结束
disp('线性相关耗用时间(s):');disp(t)%在命令行显示耗时t
%% 利用傅里叶变换性质求两序列的相关值
tic %计时开始
fx1=fft(x1,2*N-1);%求加噪信号的傅里叶变换
fh=fft(h,2*N-1);%求序列h(n)的快速傅里叶值
y1=ifft(fx1.*conj(fh));%利用上述两个序列的傅里叶变换的性质求两个序列的相关值
t1=toc;%计时结束
disp('线性相关FFT 耗用时间(s1):');disp(t1)%在命令行显示耗时t1
%% 绘图
subplot(4,1,1);
plot((0:199)/Fs,x,'k--');legend('原始信号');
subplot(4,1,2);
plot((0:199)/Fs,x1,'k-*');
legend('加噪信号');
xlabel('时间/s');
ylabel('幅度');
subplot(4,1,3);
plot((-199:199)/Fs,y1,'k--')
subplot(4,1,4);
plot((1:199)/Fs,y1(201:399),'k--')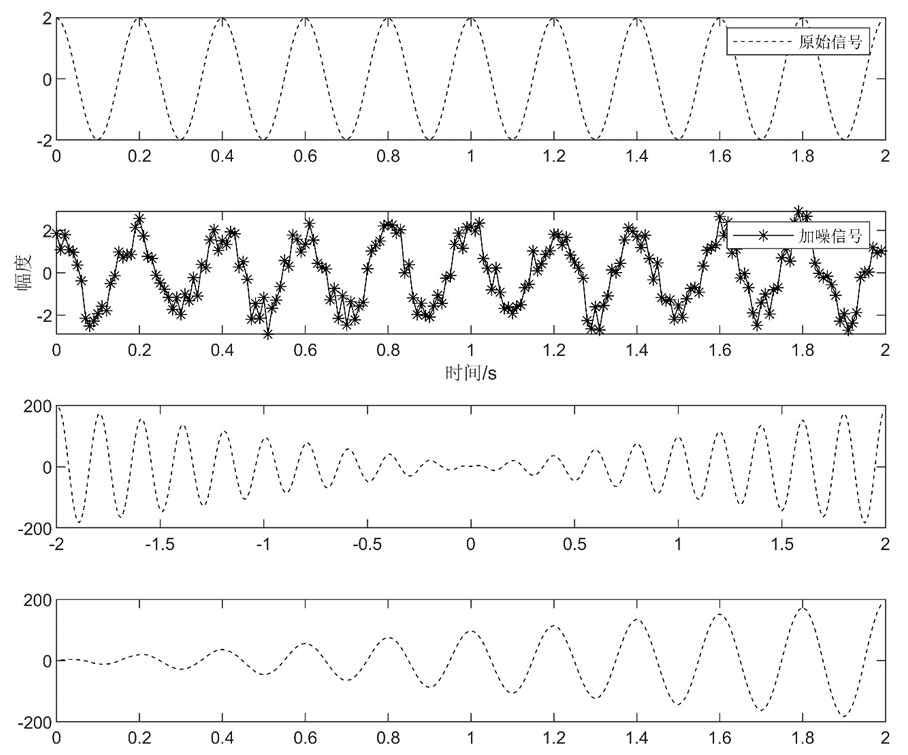
线性相关耗用时间(s):0.0062
线性相关FFT耗用时间(s1):4.9960e-04
由此可见,利用傅里叶变换性质求两序列的相关值的方法耗时远远小于直接在时域求相关值的方法。凸显了快速傅里叶变换(FFT)在信号分析处理时的优越性。
相关运算能够把信号间的共性部分提取出来,并抑制掉非共性部分,因此对噪声影响不敏感。在信号分析过程中利用相关运算可以有效地滤除噪声对于信号的影响。