数字滤波器基础

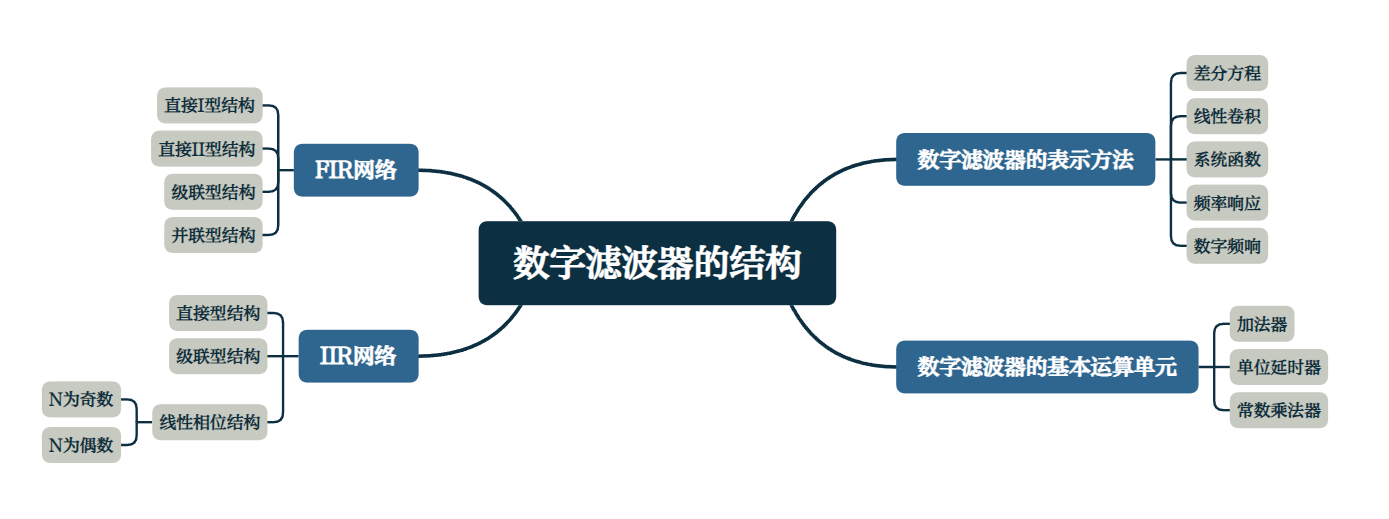
数字滤波器的表示方法

1. 时域——差分方程&线性卷积

   $$ \begin{aligned} &y(n)=\sum_{k=0}^M b_k x(n-k)+\sum_{k=1}^N a_k y(n-k) \\ &y(n)=x(n) * h(n) \end{aligned} $$

2. 复频域(Z域)——系统函数

   $$ H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{k=0}^M b_k z^{-k}}{1-\sum_{k=1}^N a_k z^{-k}} $$

3. 频域——系统频率响应

   $$ H\left(e^{j \omega}\right)=\left.H(z)\right|_{z=e^{j \omega}} $$

4. 数字频域——系统数字频响

   $$ H(k)=\left.H\left(e^{j \omega}\right)\right|_{\omega=\frac{2 \pi}{N} k} \quad(0 \leq k \leq N-1) $$

数字滤波器的功能

将输入序列经过一定的运算变换成输出序列，这种由输入到输出的运算，可以用软件或硬件实现。

基本运算单元

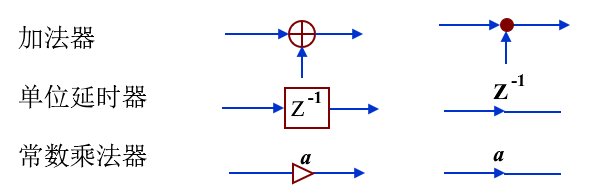
基本运算单元有：加法器、单位延时器、常数乘法器。

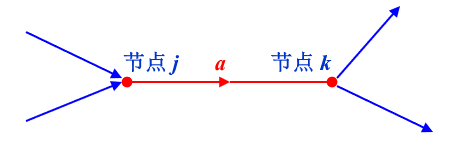
信号流图

用节点与有向支路描述系统

网络结构分类

FIR网络

不存在反馈支路，其单位脉冲响应有限长。

$$ y(n)=\sum_{i=0}^M b_i x(n-i) \quad h(n)=\left\{\begin{array}{l} b_n, 0 \leq n \leq M \\ 0 \end{array}\right. $$

IIR网络

存在反馈支路，即信号流图中存在环路，其单位脉冲响应无限长。

$$ y(n)=\sum_{i=0}^M b_i x(n-i)-\sum_{i=1}^N a_i y(n-i) $$

IIR滤波器的基本结构

IIR滤波器

系统函数

$$ H(z)=\frac{\sum_{k=0}^M b_k z^{-k}}{1-\sum_{k=1}^N a_k z^{-k}} $$

性质和特点

递归型结构；

$\boldsymbol{h}(\boldsymbol{n})$ 是无限长序列；

系统函数在有限 $\mathbf{z}$ 面上有极点, 即 $\boldsymbol{a}_k$ 不全为零。

分类

全极点系统

$b_k(k \neq 0)$ 全部为零，系统函数在有限z平面上只有极点没有零点。

零、极点系统

$b_k(k \neq 0)$ 不全为零，系统函数在有限z平面上既有极点又有零点。

直接I型结构

结构

$$ y(n)=\sum_{k=0}^M b_k x(n-k)+\sum_{k=1}^N a_k y(n-k) $$

$$ H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{k=0}^M b_k z^{-k}}{1-\sum_{k=1}^N a_k z^{-k}} $$

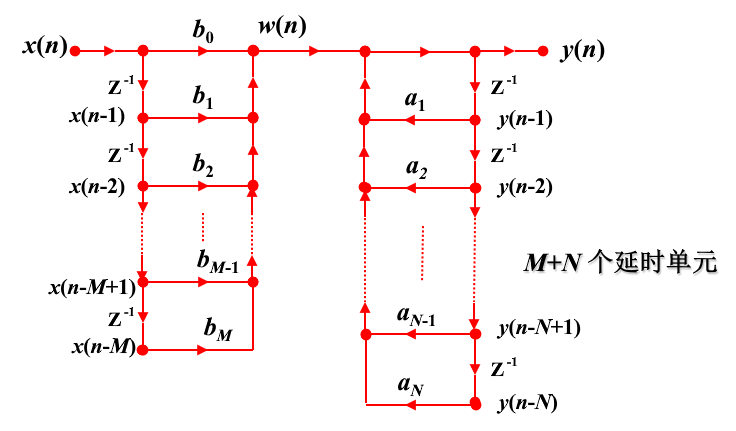
缺点

1. 需要（N+M）个延时单元，太多；
2. 系数ak、bk对滤波器性能的控制不直接，这是由于它们与极点、零点的关系不明显，因而调整困难，一个ak、bk的改
   变会影响系统所有零点或极点的分布；
3. 对字长变化敏感（对ak、bk的准确度要求严格），容易出现不稳定或产生较大误差。阶数高时，上述影响更大。

直接II型结构

结构

$$ H(z)=\frac{\sum_{k=0}^M b_k z^{-k}}{1-\sum_{k=1}^N a_k z^{-k}}=H_1(z) H_2(z)=H_2(z) H_1(z) $$

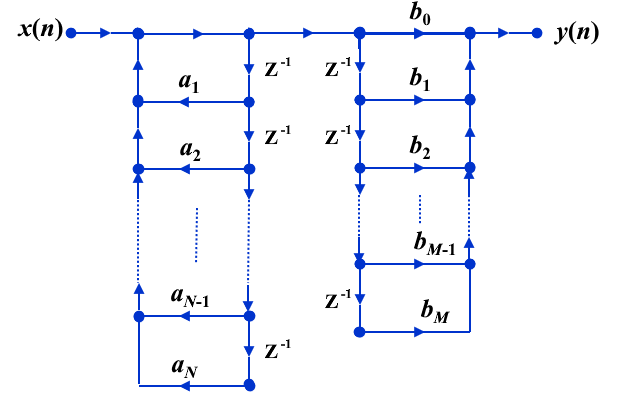
优缺点

优点：具有实现N阶滤波器所需的最少的延时单元，可节省寄存器或存储单元，所以直接Ⅱ型又称为“典范型”。

缺点：

1. 需要（N+M）个延时单元，太多；
2. 系数ak、bk对滤波器性能的控制不直接，这是由于它们与极点、零点的关系不明显，因而调整困难，一个ak、bk的改变会影响系统所有零点或极点的分布；
3. 对字长变化敏感（对ak、bk的准确度要求严格），容易出现不稳定或产生较大误差。阶数高时，上述影响更大。

转置结构

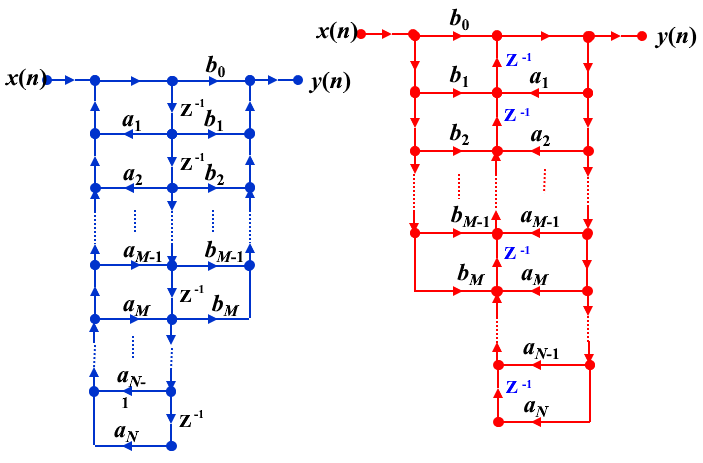
级联型结构

按零、极点将H(z)的分子和分母进行因式分解，即：

$$ \begin{aligned} H(z) &=\frac{\sum_{k=0}^M b_k z^{-k}}{1-\sum_{k=1}^N a_k z^{-k}}=A \cdot \frac{\prod_{k=1}^{M_1}\left(1-p_k z^{-1}\right) \prod_{k=1}^{M_2}\left(1-q_k z^{-1}\right)\left(1-q_k^* z^{-1}\right)}{\prod_{k=1}^{N_1}\left(1-c_k z^{-1}\right) \prod_{k=1}^{N_2}\left(1-d_k z^{-1}\right)\left(1-d_k^* z^{-1}\right)} \\ =& A \cdot \frac{\prod_{k=1}^{M_1}\left(1-p_k z^{-1}\right) \prod_{k=1}^{M_2}\left(1+\beta_{1 k} z^{-1}+\beta_{2 k} z^{-2}\right)}{\prod_{k=1}^{N_1}\left(1-c_k z^{-1}\right) \prod_{k=1}^{N_2}\left(1-\alpha_{1 k} z^{-1}-\alpha_{2 k} z^{-2}\right)} \end{aligned} $$

$$ H(z)=A \cdot \prod_k \frac{1+\beta_{1 k} z^{-1}+\beta_{2 k} z^{-2}}{1-\alpha_{1 k} z^{-1}-\alpha_{2 k} z^{-2}}=A \cdot \prod_k H_k(z) $$

其中，$\frac{1+\beta_{1 k} z^{-1}+\beta_{2 k} z^{-2}}{1-\alpha_{1 k} z^{-1}-\alpha_{2 k} z^{-2}}$为二阶基本节。

二阶基本节

$$ H_k(z)=\frac{1+\beta_{1 k} z^{-1}+\beta_{2 k} z^{-2}}{1-\alpha_{1 k} z^{-1}-\alpha_{2 k} z^{-2}} $$

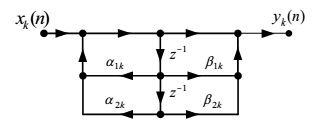
一阶基本节

$$ H_k(z)=\frac{1+\beta_{1 k} z^{-1}}{1-\alpha_{1 k} z^{-1}} $$

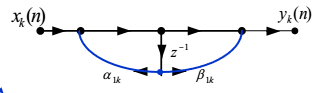
级联结构

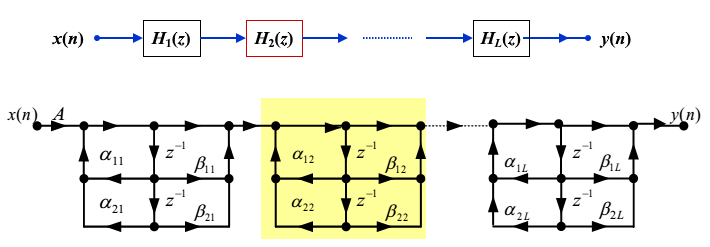
缺点

1. 各基本节的配合与排序，存在着最优化的问题；
2. 有误差累积的现象；
3. 级联各节之间须有电平的放大和缩小，以使变量值不会太大（溢出）或太小（信噪比低）。

并联型结构

将H(z)进行部分分式展开，即（一般 N≥M ）

$$ \begin{aligned} H(z) &=G_0+\sum_{k=1}^{N_1} \frac{A_k}{1-c_k z^{-1}}+\sum_{k=1}^{N_2}\left(\frac{B_k}{1-d_k z^{-1}}+\frac{B_k^*}{1-d_k^* z^{-1}}\right) \\ &=G_0+\sum_{k=1}^{N_1} \frac{A_k}{1-c_k z^{-1}}+\sum_{k=1}^{N_2} \frac{\gamma_{0 k}+\gamma_{1 k} z^{-1}}{1-\alpha_{1 k} z^{-1}-\alpha_{2 k} z^{-2}} \\ &=G_0+\sum_{k=1}^L H_k(z) \end{aligned} $$

二阶基本节

$$ H_k(z)=\frac{\gamma_{0 k}+\gamma_{1 k} z^{-1}}{1-\alpha_{1 k} z^{-1}-\alpha_{2 k} z^{-2}} $$

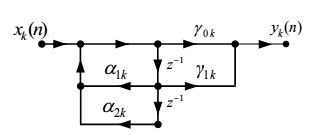
一阶基本节

$$ H_k(z)=\frac{\gamma_{0 k}}{1-\alpha_{1 k} z^{-1}} $$

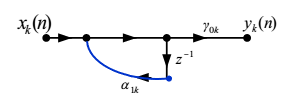
并联结构

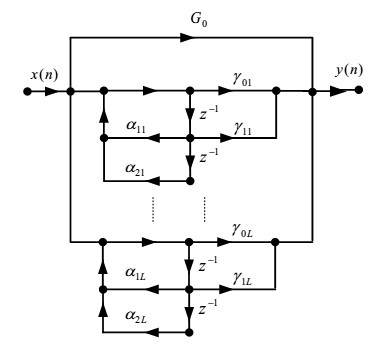
优缺点

优点：

1. 运算速度快；
2. 各并联基本节的误差互不影响，因此比级联型的误差一般说要稍小一些；
3. 可以单独调整极点的位置。

缺点：不能如级联型那样直接调整零点。

FIR数字滤波器的基本结构

FIR滤波器

系统函数

$$ H(z)=\sum_{m=0}^M b_m z^{-m}=\sum_{n=0}^M h(n) z^{-n} $$

若h(n)为N点序列，且0≤n≤N-1，则系统函数为：

$$ H(z)=\sum_{n=0}^{N-1} h(n) z^{-n} $$

特点和性质

1. h(n)是有限长序列；
2. 系统函数在有限z平面上只有零点没有极点，即 ak 全为零；
3. 非递归型结构，也可以用递归型结构实现。

分类

FIR数字滤波器即为全零点系统

直接型结构

系统函数

$$ \begin{gathered} H(z)=\sum_{n=0}^{N-1} h(n) z^{-n}=\sum_{k=0}^{N-1} b_k z^{-k} \\ y(n)=\sum_{k=0}^{N-1} b_k x(n-k) \end{gathered} $$

N个乘法器，(N-1)个延迟单元，(N-1)个加法器

级联型结构

系统函数

将H(z)分解为若干个实系数一阶、二阶因子相乘：

$$ H(z)=\prod_{k=1}^L\left(\beta_{0 k}+\beta_{1 k} z^{-1}+\beta_{2 k} z^{-2}\right)=\prod_{k=1}^L \mathrm{H}_{\mathrm{k}}(\mathrm{z}) $$

二阶基本节

$$ H_k(z)=\beta_{0 k}+\beta_{1 k} z^{-1}+\beta_{2 k} z^{-2} $$

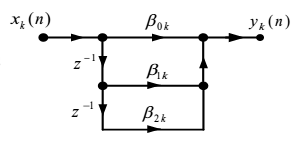
级联型结构

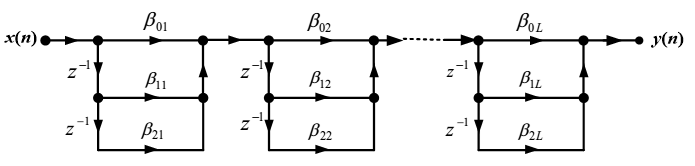
线性相位结构

线性相位条件

h(n)为N点有限长实数序列，0≤ n ≤N-1,且满足偶对称或奇对称，即：

1. 偶对称：$h(n)=h(N-1-n)$
2. 奇对称：$h(n)=-h(N-1-n)$

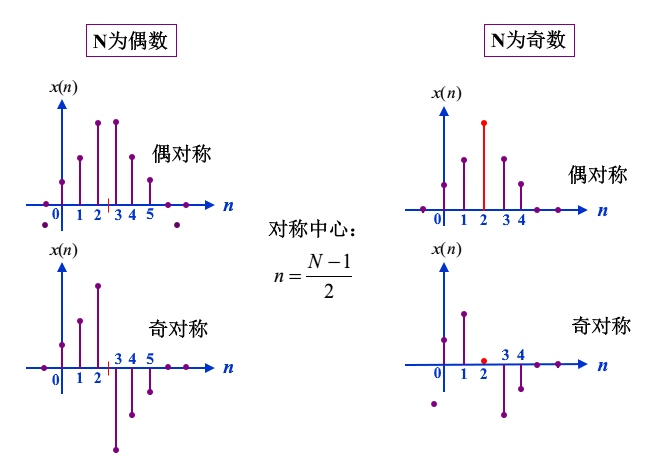
N为偶数时

$$ \begin{aligned} H(z) &=\sum_{n=0}^{N-1} h(n) z^{-n}=\sum_{n=0}^{\frac{N}{2}-1} h(n) z^{-n}+\sum_{n=\frac{N}{2}}^{N-1} h(n) z^{-n} \\ &=\sum_{n=0}^{\frac{N}{2}-1} h(n) z^{-n}+\sum_{m=0}^{\frac{N}{2}-1} h(N-1-m) z^{-(N-1-m)} \\ H(z) &=\sum_{n=0}^{\frac{N}{2}-1} h(n)\left[z^{-n} \pm z^{-(N-1-n)}\right] \end{aligned} $$

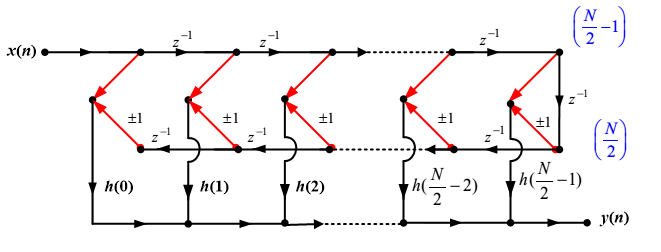
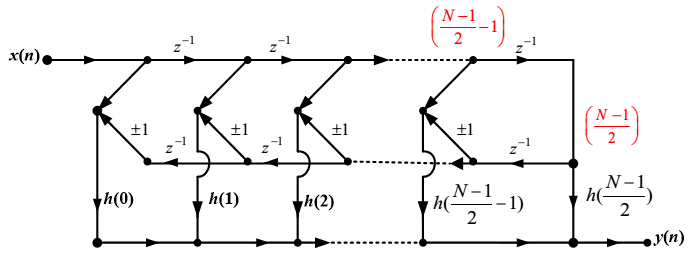
N为奇数时

$$ \begin{aligned} H(z) &=\sum_{n=0}^{N-1} h(n) z^{-n}=\sum_{n=0}^{\frac{N-1}{2}-1} h(n) z^{-n}+h\left(\frac{N-1}{2}\right) z^{-\frac{N-1}{2}}+\sum_{n=\frac{N-1}{2}+1}^{N-1} h(n) z^{-n} \\ &=\sum_{n=0}^{\frac{N-1}{2}-1} h(n) z^{-n}+h\left(\frac{N-1}{2}\right) z^{-\frac{N-1}{2}}+\sum_{n=0}^{\frac{N-1}{2}-1} h(N-1-n) z^{-(N-1-n)} \\ &=\sum_{n=0}^{\frac{N-1}{2}-1} h(n)\left[z^{-n} \pm z^{-(N-1-n)}\right]+h\left(\frac{N-1}{2}\right) z^{-\frac{N-1}{2}} \end{aligned} $$