实验目的
1.了解常用的时域离散信号及其特点。
2.掌握 MATLAB 产生常用时域离散信号的方法。
3.掌握离散时间序列时域的基本运算方法。
4.掌握 MATLAB 语言进行离散序列运算的常用函数,掌握离散序列运算程序的编写方法。
实验环境
Windows 11 , MATLAB2021a
示例程序
(1)单位抽样序列$\delta(n)$
%用MATLAB的关系运算式来产生单位抽样序列δ(n)
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
n1=-5;n2=5;n0=0;%新建变量及赋值
n=n1:n2;%创建范围由n1到n2且步长为1的行矩阵
x=[n==n0];%除了在n=n0=0处将x赋值为true(1),别处均将x赋值为false(0)
stem(n,x,'filled');%绘制离散序列数据图
axis([n1,n2,0,1.1*max(x)]);%图轴范围
title('单位脉冲序列');%图名
xlabel('时间(n)');ylabel('幅度 x(n)')%图横纵坐标名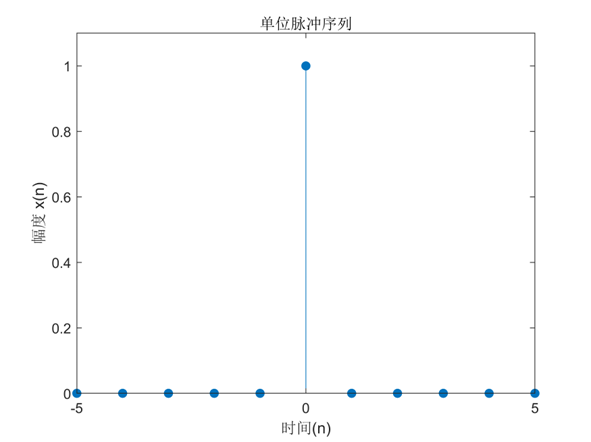
(2)单位阶跃序列$u(n)$
%用MATLAB的关系运算式来产生单位阶跃序列u(n)
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
n1=-2;n2=8;n0=0;%新建变量及赋值
n=n1:n2;%创建范围由n1到n2且步长为1的行矩阵
x=[n>=n0];%在n>=n0=0处将x赋值为true(1),别处将x赋值为false(0)
stem(n,x,'filled');%绘制离散序列数据图
axis([n1,n2,0,1.1*max(x)]);%图轴范围
title('单位阶跃序列');%图名
xlabel('时间(n)');ylabel('幅度 x(n)')%图横纵坐标名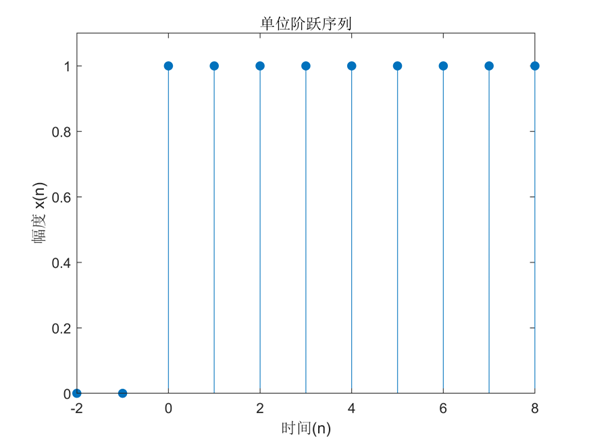
(3)复指数信号及采样
编写产生$\sigma=-0.1, w=0.6$的复指数连续时间信号和离散序列的程序
%编写产生σ=-0.1、w=0.6复指数连续时间信号和离散序列的程序
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
n1=30;a=-0.1;w=0.6;%新建变量及赋值
n=0:n1;%创建范围由0到n1且步长为1的行矩阵
x=exp((a+j*w)*n);%复指数原信号
subplot(2,2,1);%绘制两行两列的一组图中的第一幅图
plot(n,real(x));%绘制“x实部-n”二维线图
title('复指数原信号的实部');%图名
subplot(2,2,2);%绘制两行两列的一组图中的第二幅图
stem(n,real(x),'filled');%绘制“x实部-n”离散序列数据图
title('复指数原信号的实部');%图名
subplot(2,2,3);%绘制两行两列的一组图中的第三幅图
plot(n,imag(x));%绘制“x虚部-n”二维线图
title('复指数原信号的虚部');%图名
subplot(2,2,4);%绘制两行两列的一组图中的第四幅图
stem(n,imag(x),'filled');%绘制“x虚部-n”离散序列数据图
title('复指数原信号的虚部');%图名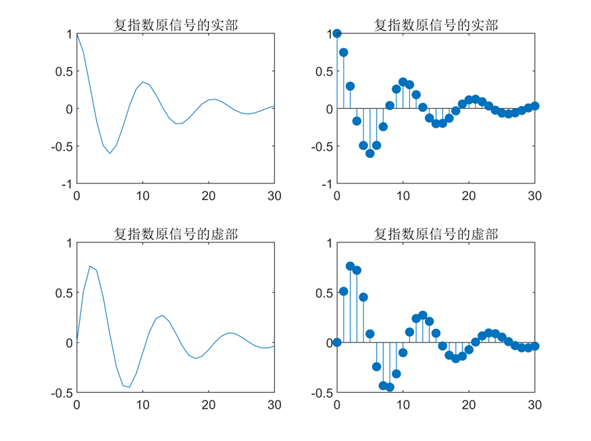
(4)正弦信号及采样
已知一时域周期性正弦信号的频率为1Hz,振幅值幅度为1V。在窗口上显示2个周期的信号波形,并对信号幅度$x(n)$的一个周期进行32点采样获得离散信号。试显示原连续信号和其采样获得的离散信号波形。
% 已知一时域周期性正弦信号的频率为1Hz,振幅值幅度为1V。
% 在窗口上显示2个周期的信号波形,并对信号幅度x(n)的一个周期进行32点采样获得离散信号。
% 试显示原连续信号和其采样获得的离散信号波形。
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
f=1;Um=1;nt=2;%新建变量及赋值
N=32;T=1/f;;%新建变量及赋值
dt=T/N;%计算采样时间间隔
n=0:nt*N-1;%计算总采样点数,并形成行矩阵
tn=n*dt;%计算每个采样点对应的时域时刻,并形成行矩阵
x=Um*sin(2*f*pi*tn);%正弦信号
subplot(2,1,1);plot(tn,x);%绘制原信号图
axis([0 nt*T 1.1*min(x) 1.1*max(x)]);%图轴范围设置
ylabel('x(t)');%y轴名称
subplot(2,1,2);stem(tn,x);%绘制采样后信号图
axis([0 nt*T 1.1*min(x) 1.1*max(x)]);%图轴范围设置
ylabel('x(t)');%y轴名称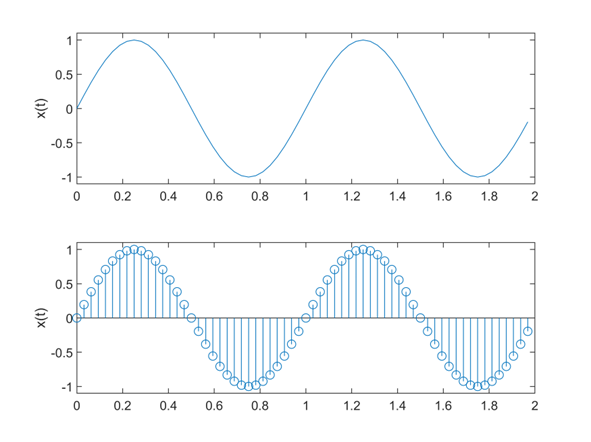
(5)矩形波信号及采样
已知一连续的周期性矩形波信号的频率为5kHz,振幅值幅度为0~2V。脉冲宽度与周期的比例为1:4,且在窗口上显示2个周期的信号波形,并对信号的一个周期进行16点采样获得离散信号。
% 已知一连续的周期性矩形波信号的频率为5kHz,振幅值幅度为0~2V。
% 脉冲宽度与周期的比例为1:4,且在窗口上显示2个周期的信号波形,
% 并对信号的一个周期进行16点采样获得离散信号。
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
f=5000;nt=2;%新建变量及赋值
N=16;T=1/f;%新建变量及赋值
dt=T/N;%计算采样时间间隔
n=0:nt*N-1;%计算总采样点数,并形成行矩阵
tn=n*dt;%计算每个采样点对应的时域时刻,并形成行矩阵
x=square(2*f*pi*tn,25)+1;%生成矩形波
subplot(2,1,1);plot(tn,x);%绘制原信号图
axis([0 nt*T 1.1*min(x) 1.1*max(x)]);%图轴范围设置
ylabel('x(t)');%y轴名称
subplot(2,1,2);stem(tn,x);%绘制采样后信号图
axis([0 nt*T 1.1*min(x) 1.1*max(x)]);%图轴范围设置
ylabel('x(n)')%y轴名称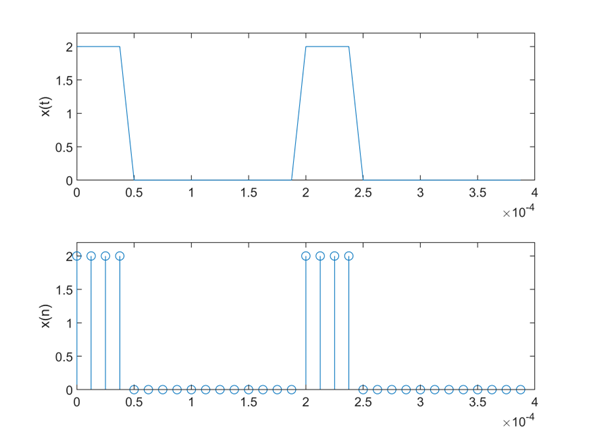
(6)序列的移位
已知$u(n)$为单位阶跃序列,$X_1(n)=u(n+6) (-10<n<10);X_2(n)=u(n-4)$$ (-10<n<10)$,对$u(n)$进行移位得到这些序列,并比较三个序列之间的关系。
% 已知u(n)为单位阶跃序列,X1(n)=u(n+6) (-10<n<10);X2(n)=u(n-4) (-10<n<10)
% 对u单位阶跃序列(n)进行移位,并比较三个序列之间的关系
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
n1=-10;n2=10;%新建变量及赋值
k0=0;k1=-6;k2=4;%新建变量及赋值
n=n1:n2;%创建范围由n1到n2且步长为1的行矩阵
x0=[n>=k0];%在n>=k0处将x0赋值为true(1),别处将x0赋值为false(0)
x1=[(n-k1)>=0];%在(n-k1)>=0处将x1赋值为true(1),别处将x1赋值为false(0)
x2=[(n-k2)>=0];%在(n-k2)>=0处将x2赋值为true(1),别处将x2赋值为false(0)
subplot(3,1,1),stem(n,x0,'filled','k');%u(n)绘图
axis([n1,n2,1.1*min(x0),1.1*max(x0)]);
ylabel('u(n)');
subplot(3,1,2),stem(n,x1,'filled','k');%u(n+6)绘图
axis([n1,n2,1.1*min(x1),1.1*max(x1)]);
ylabel('u(n+6)');
subplot(3,1,3),stem(n,x2,'filled','k');%u(n-4)绘图
axis([n1,n2,1.1*min(x2),1.1*max(x2)]);
ylabel('u(n-4)');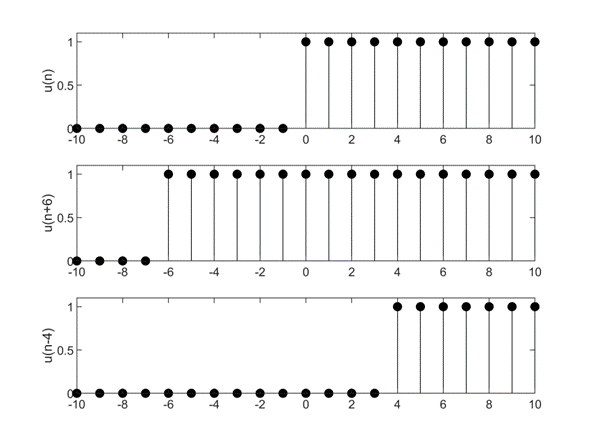
(7)相加运算
已知$u(n)$为单位阶跃序列,$x_1(n)=u(n+2)(-4<n<6) ;$$ x_2(n)=u(n-4)(-5<n<8)$,求$x(n)=x_1(n)+x_2(n)$的相加运算。
% 已知u(n)为单位阶跃序列,x1(n)=u(n+2)(-4<n<6) ; x2(n)=u(n-4) (-5<n<8)
% 求x(n)=x1(n)+x2(n)的相加运算
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
n1=-4:6;n01=-2;%新建变量及赋值
x1=[(n1-n01)>=0];%在(n1-n01)>=0处将x1赋值为true(1),别处将x1赋值为false(0)
n2=-5:8;n02=4;%新建变量及赋值
x2=[(n2-n02)>=0];%在(n2-n02)>=0处将x2赋值为true(1),别处将x2赋值为false(0)
n=min([n1,n2]):max([n1,n2]); %为 x 信号建立时间序列 n
N=length(n);%测时间序列n的长度
y1=zeros(1,N);y2=zeros(1,N);%创建长度为N的全零行矩阵
y1(find((n>=min(n1))&(n<=max(n1))))=x1;%把x1赋值进y1
y2(find((n>=min(n2))&(n<=max(n2))))=x2;%把x2赋值进y2
x=y1+y2;%相加
%% 绘图
subplot(3,1,1),stem(n1,x1,'filled','k');
%axis([n1,n2,1.1*min(x0),1.1*max(x0)]);
ylabel('x1(n)');
subplot(3,1,2),stem(n2,x2,'filled','k');
%axis([n1,n2,1.1*min(x1),1.1*max(x1)]);
ylabel('x2(n)');
subplot(3,1,3),stem(n,x,'filled');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);
ylabel('x(n)');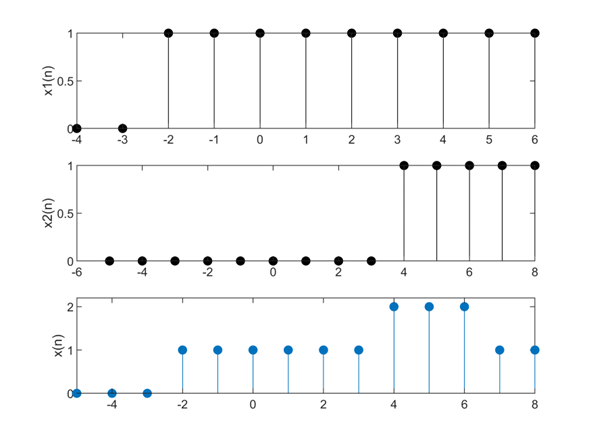
(8)复指数序列
$ f(n)=e^{(0.1+j1.6π)n } (0<=n<=16)$
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
n1=16;a=0.1;w=1.6*pi;%新建变量及赋值
n=0:n1;%创建范围由0到n1且步长为1的行矩阵
x=exp((a+j*w)*n);%复指数原信号
subplot(2,2,1);%绘制两行两列的一组图中的第一幅图
plot(n,real(x));%绘制“x实部-n”二维线图
title('复指数原信号的实部');%图名
subplot(2,2,2);%绘制两行两列的一组图中的第二幅图
stem(n,real(x),'filled');%绘制“x实部-n”离散序列数据图
title('复指数原信号的实部');%图名
subplot(2,2,3);%绘制两行两列的一组图中的第三幅图
plot(n,imag(x));%绘制“x虚部-n”二维线图
title('复指数原信号的虚部');%图名
subplot(2,2,4);%绘制两行两列的一组图中的第四幅图
stem(n,imag(x),'filled');%绘制“x虚部-n”离散序列数据图
title('复指数原信号的虚部');%图名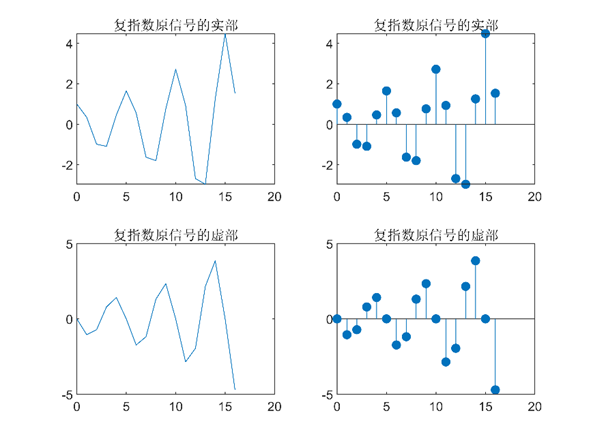
(9)正弦序列
$f(n)=3 \cos \frac{n \pi}{4}(0<=n<=20)$
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
w=pi/4;Um=3;%新建变量及赋值
n1=20;%新建变量及赋值
n=0:n1;%创建范围由0到n1且步长为1的行矩阵
x=Um*cos(w*n);%正弦信号
%% 绘图
subplot(1,2,1);
plot(n,x);
title('原信号');
subplot(1,2,2);
stem(n,x,'filled');
title('离散信号');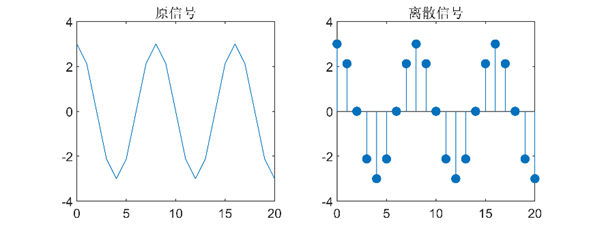
(10)相加运算-2
$x(n)=u(n+2)+u(n-2)$,$(-5<=n<=5)$
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
n1=-5:5;n01=-2;%新建变量及赋值
x1=[(n1-n01)>=0];%在(n1-n01)>=0处将x1赋值为true(1),别处将x1赋值为false(0)
n2=-5:5;n02=2;%新建变量及赋值
x2=[(n2-n02)>=0];%在(n2-n02)>=0处将x2赋值为true(1),别处将x2赋值为false(0)
n=min([n1,n2]):max([n1,n2]); %为x信号建立时间序列n
N=length(n);%测时间序列n的长度
y1=zeros(1,N);y2=zeros(1,N);%创建长度为N的全零行矩阵
y1(find((n>=min(n1))&(n<=max(n1))))=x1;%把x1赋值进y1
y2(find((n>=min(n2))&(n<=max(n2))))=x2;%把x2赋值进y2
x=y1+y2;%相加
%% 绘图
subplot(3,1,1),stem(n1,x1,'filled','k');
%axis([n1,n2,1.1*min(x0),1.1*max(x0)]);
ylabel('x1(n)');
subplot(3,1,2),stem(n2,x2,'filled','k');
%axis([n1,n2,1.1*min(x1),1.1*max(x1)]);
ylabel('x2(n)');
subplot(3,1,3),stem(n,x,'filled');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);
ylabel('x(n)');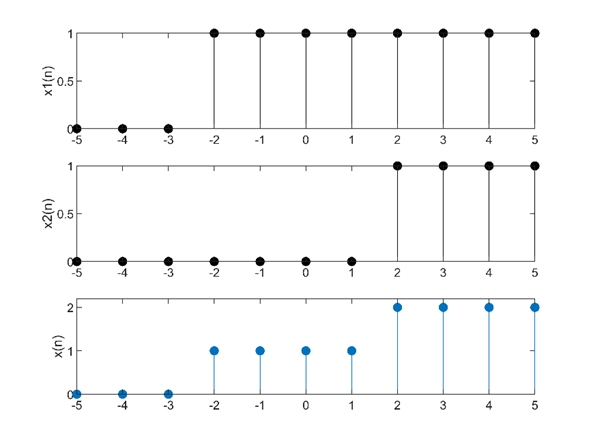
(11)矩形波信号及采样-2
已知一连续周期性方波信号的频率为 200Hz,振幅值幅度为-1V到1V之间。在窗口上显示2个周期的信号波形,用Fs=4kHz的频率对连续信号进行采样。试显示原连续信号和其采样获得的离散信号波形。
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
f=200;nt=2;%新建变量及赋值
fs=4000;N=fs/f;T=1/f;%新建变量及赋值
dt=T/N;%计算采样时间间隔
n=0:nt*N-1;%计算总采样点数,并形成行矩阵
tn=n*dt;%计算每个采样点对应的时域时刻,并形成行矩阵
x=square(2*f*pi*tn,50);%生成方波
subplot(2,1,1);plot(tn,x);%绘制原信号图
axis([0 nt*T 1.1*min(x) 1.1*max(x)]);%图轴范围设置
ylabel('x(t)');%y轴名称
subplot(2,1,2);stem(tn,x);%绘制采样后信号图
axis([0 nt*T 1.1*min(x) 1.1*max(x)]);%图轴范围设置
ylabel('x(n)')%y轴名称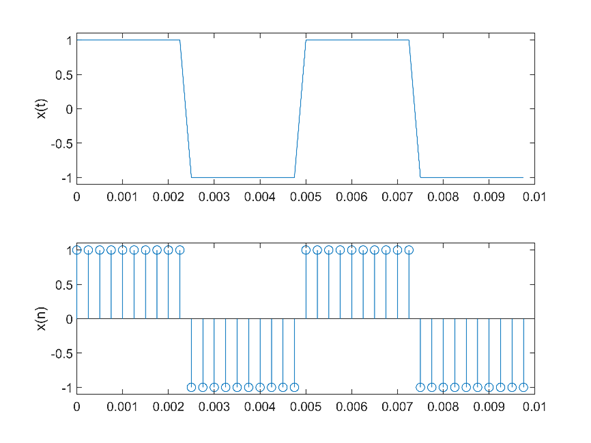
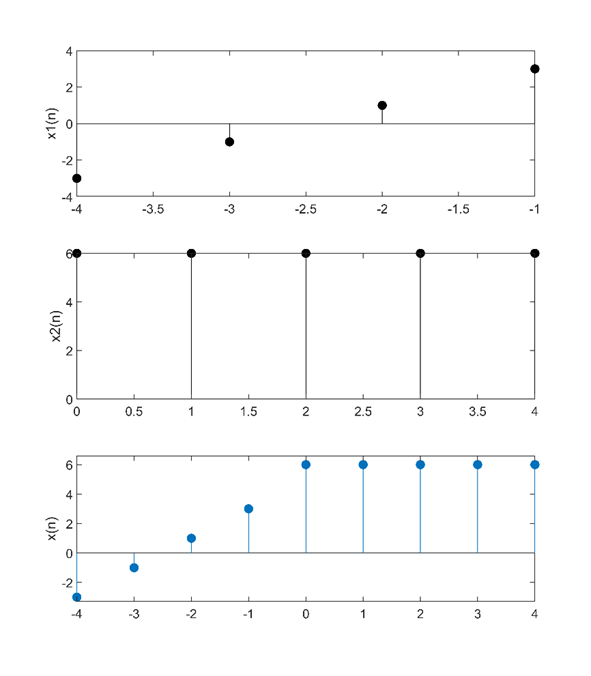
(12)复合序列
$x(n)= \begin{cases}2 n+5 & (-4 \leq n \leq-1) \\ 6 & (0 \leq n \leq 4) \\ 0 & \text { 其它 }\end{cases}$
% 已知u(n)为单位阶跃序列,x1(n)=u(n+2)(-4<n<6) ; x2(n)=u(n-4) (-5<n<8)
% 求x(n)=x1(n)+x2(n)的相加运算
close all;clc;clear;%关闭所有之前的窗口,清除所有变量,清空命令行
n1=-4:-1;%新建变量及赋值
x1=2*n1+5;
n2=0:4;%新建变量及赋值
x2(find((n2>=min(n2))&(n2<=max(n2))))=6;%取值范围内全部取6
n=min([n1,n2]):max([n1,n2]); %为 x 信号建立时间序列 n
N=length(n);%测时间序列n的长度
y1=zeros(1,N);y2=zeros(1,N);%创建长度为N的全零行矩阵
y1(find((n>=min(n1))&(n<=max(n1))))=x1;%把x1赋值进y1
y2(find((n>=min(n2))&(n<=max(n2))))=x2;%把x2赋值进y2
x=y1+y2;%相加
%% 绘图
subplot(3,1,1),stem(n1,x1,'filled','k');
%axis([n1,n2,1.1*min(x0),1.1*max(x0)]);
ylabel('x1(n)');
subplot(3,1,2),stem(n2,x2,'filled','k');
%axis([n1,n2,1.1*min(x1),1.1*max(x1)]);
ylabel('x2(n)');
subplot(3,1,3),stem(n,x,'filled');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);
ylabel('x(n)');