序列
序列的运算
基本运算
- 加法:$x(n)+y(n)=z(n)$
- 乘法:$x(n)^* y(n)=z(n)$
- 累加:$\mathrm{y}(\mathrm{n})=\sum_{k=-\infty}^n x(k)$
- 前向差分:$\Delta {x}({n})={x}({n}+1)-{x}({n})$
- 后向差分:$\nabla {x}({n})={x}({n})-{x}({n}-1)$
- 移位:$x(n) \rightarrow x(n\pm m)$
- 翻转:$x(n) \rightarrow x(-n)$
- 卷积:$x(n) * h(n)=\sum_{m=-\infty}^{\infty} x(m) h(n-m)$
卷积
定义式
$$ x(n) * h(n)=\sum_{m=-\infty}^{\infty} x(m) h(n-m) $$
常用卷积
$$ \delta(n) * x(n)=x(n), \quad \delta(n-m) * x(n)=x(n-m) $$
应用
$$ \begin{array}{lll} \text { (1) } x(n)=\delta(n) & , & h(n)=R_5(n) \\ \text { (2) } x(n)=R_3(n) & , & h(n)=R_4(n) \\ \text { (3) } x(n)=\delta(n-2)&, &h(n)=0.5^n R_3(n) \end{array} $$
(1) $y(n)=x(n) * h(n)=R_5(n)$
(2) $y(n)=x(n) * h(n)=\{1,2,3,3,2,1\}$
(3) $y(n)=\delta(n-2) * 0.5^n R_3(n)=0.5^{n-2} R_3(n-2)$
常见的序列
- 单位抽样序列:$\delta(n)$
- 周期冲激序列:$\delta_T(t)=\sum_{n=-\infty}^{\infty} \delta(t-n T)$
- 单位阶跃序列:$u(n)$,$\delta(n)=u(n)-u(n-1)$,$u(n)=\delta(n)+\delta(n-1)+\delta(n-2)+\ldots=\sum_{m=0}^{\infty} \delta(n-m)$
- 矩形序列:$R_N(n)= \begin{cases}1 & 0 \leq n \leq N-1 \\ 0 & \text { 其他 }\end{cases}$
- 实指数序列:$x(n)=a^n u(n)$,若 $|a|<1$ 序列收敛, 若 $|a|>1$ 序列发散
- 虚指数序列:$x(n)=e^{\left(\sigma+j \omega_0\right) n}=e^{\sigma \cdot n} e^{j \omega_0 n}=e^{\sigma \cdot n}\left(\cos \omega_0 n+j \sin \omega_0 n\right)$
- 正弦序列:$x(n)=A \sin \left(n \omega_0+\phi\right)$,其中 $\omega_0$ 为数字频率
序列的周期
- $\frac{2 \pi}{\omega_0}=N$ 为整数时, $\mathrm{x}(\mathrm{n})$ 为周期序列,周期为$\mathrm{N}$;
- $\frac{2 \pi}{\omega_0}=\frac{P}{Q}$ 为有理数时, $\mathrm{x}(\mathrm{n})$ 为周期序列,周期为 $\mathrm{N}=\mathrm{P}$;
- $\frac{2 \pi}{\omega_0}$ 的结果为无理数(通常带有$\pi$) 时,不是周期序列。
应用
判断是否为周期序列:
$$ \begin{gathered} (a) x(n)=A \cos \left(\frac{3 \pi}{7} n-\frac{\pi}{8}\right) \\ 2 \pi / \omega_0=2 \pi / \frac{3 \pi}{7}=\frac{14}{3} \end{gathered} $$
$\therefore$ 是周期的,周期为14;
$$ \begin{aligned} &(b) x(n)=A \sin \left(\frac{13}{3} \pi n\right) \\ &2 \pi / \omega_0=2 \pi / \frac{13}{3} \pi=\frac{6}{13} \end{aligned} $$
$\therefore$ 是周期的, 周期是6。
线性时不变系统
线性
线性=齐次性&可加性
$a_1 y_1(n)+a_2 y_2(n)=a_1 T\left[x_1(n)\right]+a_2 T\left[x_2(n)\right]=T\left[a_1 x_1(n)\right]+T\left[a_2 x_2(n)\right]$
时不变
$T[x(n)]=y(n)$ ,则 $T\left[x\left(n-n_0\right)\right]=y\left(n-n_0\right)$
应用
试判断以下每一系统是否是线性、移不变的?
(1) $T[x(n)]=g(n) x(n)$
线性判断:
$\begin{aligned} & T[x(n)]=g(n) x(n) \\ & T\left[a x_1(n)+b x_2(n)\right] \\=& g(n)\left[a x_1(n)+b x_2(n)\right] \\=& g(n) \times a x_1(n)+g(n) \times b x_2(n) \\=& a T\left[x_1(n)\right]+b T\left[x_2(n)\right] \end{aligned}$
所以是线性系统。
移不变判断:
$\begin{aligned} T[x(n-m)] &=g(n) x(n-m) \\ y(n-m) &=g(n-m) x(n-m) \\ T[x(n-m)] & \neq y(n-m) \end{aligned}$
所以不是移不变。
(2)$T[x(n)]=\sum_{\mathrm{k}=\mathrm{n}_0}^{\mathrm{n}} x(k)$
线性判断:
$T[x(n)]=\sum_{k=n_0}^n x(k)$
$=\sum_{k=n_0}^n\left[a x_1(k)+b x_2(k)\right]$
$=\sum_{k=n_0}^n a x_1(k)+\sum_{k=n_0}^n b x_2(k)$
$=a T\left[x_1(n)\right]+b T\left[x_2(n)\right]$
所以是线性。
移不变判断:
$\begin{aligned} T[x(n-m)] &=\sum_{k=n_0}^n x(k-m) \\ &=\sum_{k=n_0-m}^{n-m} x(k) \\ y(n-m) &=\sum_{k=n_0}^{n-m} x(k) \\ T[x(n-m)] & \neq y(n-m) \end{aligned}$
所以不是移不变。
因果和稳定
因果系统
系统的输出不超前输入,即n时刻的输出仅与n时刻及其之前的时刻有关。
判定方法:在$n<0$时,$h(n)=0$
稳定系统
有界输入产生有界输出
判定方法:$\sum_{n=-\infty}^{\infty}|h(n)|=P<\infty$
DTFT
DTFT
定义
$$ X\left(e^{j \omega}\right)=\operatorname{DTFT}[x(n)]=\sum_{n=-\infty}^{\infty} x(n) e^{-j \omega \cdot n} $$
$$ x(n)=\mathrm{I D T F T}\left[X\left(e^{j \omega}\right)\right]=\frac{1}{2 \pi} \int_{-\pi}^\pi X\left(e^{j \omega}\right) \cdot e^{j \omega n} d \omega $$
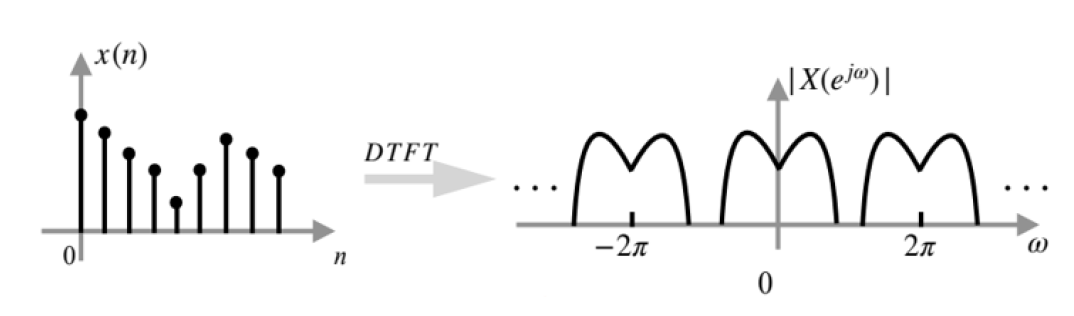
存在条件:$\sum_{n=-\infty}^{+\infty}|x(n)|<+\infty$
时频周期离散对应关系
| $x(n)$ | $X(e^{j\omega})$ |
|---|---|
| 离散 | 周期 |
| 非周期 | 连续 |
常用序列的DTFT
| 时域序列 | 频域序列 | ||||
|---|---|---|---|---|---|
| $x(n)$ | $X\left(e^{j \omega}\right)$ | ||||
| $\delta (n-n_0)$ | $e^{-j \omega-n_0}$ | ||||
| $R_N(n)$ | $\frac{\sin (N \omega / 2)}{\sin (\omega / 2)} e^{-j\left(\frac{N-1}{2}\right) \omega}$ | ||||
| $\frac{\sin \omega_c n}{\pi n}$ | $X\left(e^{j \omega}\right)= \begin{cases}1 & | \omega | <\omega_c \ 0 & \omega_c< | \omega | <\pi\end{cases}$ |
| $\delta(n)$ | $1$ |
DTFT的性质
基本性质
- 线性:$a x(n) \pm b y(n) \Leftrightarrow a X\left(e^{j \omega}\right) \pm b Y\left(e^{j \omega}\right)$
- 时移性质:$x(n-m) \Leftrightarrow e^{-j \omega m} X\left(e^{j \omega}\right)$
- 频移性质:$e^{j \omega_0 n} x(n) \Leftrightarrow X\left(e^{j\left(\omega-\omega_0\right)}\right)$
- 时域卷积:$x(n) * h(n) \Leftrightarrow X\left(e^{j \omega}\right) H\left(e^{j \omega}\right)$
- 频域卷积:$x(n) \cdot h(n) \Leftrightarrow \frac{1}{2 \pi} X\left(e^{j \omega}\right) * H\left(e^{j \omega}\right)$
- 微分:$n x(n) \Leftrightarrow j \frac{d X\left(e^{j \omega}\right)}{d \omega}$
- 帕塞瓦定理:$\sum_{n=-\infty}^{\infty}|x(n)|^2=\frac{1}{2 \pi} \int_{-\pi}^\pi\left|X\left(e^{j \omega}\right)\right|^2 d \omega$
- 反转:$x(-n) \Leftrightarrow X\left(e^{-j \omega}\right)$
- 共轭:$x^*(n) \Leftrightarrow X^*\left(e^{-j \omega}\right)$
- $\left.\begin{array}{l}x(-n) \Leftrightarrow X\left(e^{-j \omega}\right) \\ x^*(n) \Leftrightarrow X^*\left(e^{-j \omega}\right)\end{array}\right\} x^*(-n) \Leftrightarrow X^*\left(e^{j \omega}\right)$
对称性质
共轭对称与共轭反对称
共轭对称序列:$x_e(n):x_e(n)=x_e *(-n)$ 实部偶对称,虚部奇对称(实偶虚奇)
共轭反对称序列:$x_o(n):x_o(n)=-x_o *(-n)$ 实部奇对称,虚部偶对称(实奇虚偶)
对任意序列$x(n)$有:$x(n)=x_e(n)+x_o(n)$
其中:
$x_e(n)=\frac{1}{2}\left[x(n)+x^*(-n)\right]$
$x_o(n)=\frac{1}{2}\left[x(n)-x^*(-n)\right]$
同理在频域中:
$$ X\left(e^{j \omega}\right)=X_e\left(e^{j \omega}\right)+X_o\left(e^{j \omega}\right) \rightarrow\left\{\begin{array}{l} X_e\left(e^{j \omega}\right)=\frac{1}{2}\left[X\left(e^{j \omega}\right)+X^*\left(e^{-j \omega}\right)\right] \\ X_o\left(e^{j \omega}\right)=\frac{1}{2}\left[X\left(e^{j \omega}\right)-X^*\left(e^{-j \omega}\right)\right] \end{array}\right. $$
$$ \begin{aligned} &x_e(n)=\frac{1}{2}\left[x(n)+x^*(-n)\right] \Leftrightarrow \operatorname{Re}\left[X\left(e^{j \omega}\right)\right] \\ &x_o(n)=\frac{1}{2}\left[x(n)-x^*(-n)\right] \Leftrightarrow j \operatorname{Im}\left[X\left(e^{j \omega}\right)\right] \\ &x(n)=\operatorname{Re}[x(n)]+j \operatorname{Im}[x(n)]=x_e(n)+x_o(n) \\ &X\left(e^{j \omega}\right)=X_e\left(e^{j \omega}\right)+X_o\left(e^{j \omega}\right)=\operatorname{Re}\left[X\left(e^{j \omega}\right)\right]+j \cdot \operatorname{Im}\left[X\left(e^{j \omega}\right)\right] \\ & \end{aligned} $$